Evaluates a light that is a linear interpolation between two colors over the sphere.
HRESULT D3DXSHEvalHemisphereLight( UINT Order, CONST D3DXVECTOR3 * pDir, D3DXCOLOR Top, D3DXCOLOR Bottom, FLOAT * pROut, FLOAT * pGOut, FLOAT * pBOut );
If the function succeeds, the return value is D3D_OK. If the function fails, the return value can be: D3DERR_INVALIDCALL.
The interpolation is done linearly between the two points, not over the surface of the sphere (that is, if the axis was (0,0,1) it is linear in Z, not in the azimuthal angle). The resulting spherical lighting function is normalized so that a point on a perfectly diffuse surface with no shadowing and a normal pointed in the direction pDir would result in exit radiance with a value of 1 (if the top color was white and the bottom color was black). This is a very simple model where Top represents the intensity of the "sky" and Bottom represents the intensity of the "ground."
On the sphere with unit radius as shown, direction can be specified simply with theta, the angle about the z-axis in the right-handed direction, and phi, the angle from z.
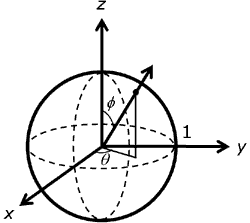
The following equations show the relationship between Cartesian (x, y, z) and spherical (theta, phi) coordinates on the unit sphere. The angle theta varies over the range of 0 to 2 pi, while phi varies from 0 to pi.
Header: Declared in D3dx9math.h.