There are four wrapping types:
·Flat
·Cylindrical
·Spherical
·Chrome
This section describes these wrapping types. In the examples, the direction vector (the v vector) lies along the z-axis, and the up vector (the u vector) lies along the y-axis, with the origin at [0 0 0].
Flat
The flat wrap conforms to the faces of an object as if the texture were a piece of rubber that was stretched over the object.
The [u v] coordinates are derived from a vector [x y z] by using the following equations:
u=sux–ou
v=svy–ov
In these formulas, s is the window-scaling factor and o is the window origin. The application should choose a pair of scaling factors and offsets that map the ranges of x and y to the range from 0 to 1 for u and v.
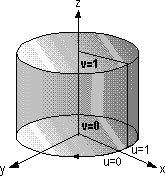
Cylindrical
The cylindrical wrap treats the texture as if it were a piece of paper that is wrapped around a cylinder so that the left edge is joined to the right edge. The object is then placed in the middle of the cylinder and the texture is deformed inward onto the surface of the object.
For a cylindrical texture map, the effects of the various vectors are shown in the following illustration.

The direction vector specifies the axis of the cylinder, and the up vector specifies the point on the outside of the cylinder where u equals 0. To calculate the texture [u v] coordinates for a vector [x y z], the system uses the following equations:
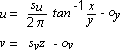
Typically, u would be left unscaled and v would be scaled and translated so that the range of z maps to the range from 0 to 1 for v.
Spherical
For a spherical wrap, the u-coordinate is derived from the angle that the vector [x y 0] makes with the x-axis (as in the cylindrical map) and the v-coordinate from the angle that the vector [x y z] makes with the z-axis. Note that this mapping causes distortion of the texture at the z-axis.
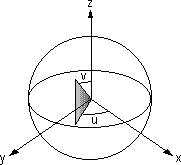
This translates to the following equations:
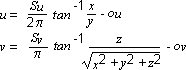
The scaling factors and texture origin will often not be needed here as the unscaled range of u and v is already 0 through 1.
Chrome
A chrome wrap allocates texture coordinates so that the texture appears to be reflected onto the objects. The chrome wrap takes the reference frame position and uses the vertex normals in the mesh to calculate reflected vectors. The texture u- and v-coordinates are then calculated from the intersection of these reflected vectors with an imaginary sphere that surrounds the mesh. This gives the effect of the mesh reflecting whatever is wrapped on the sphere.