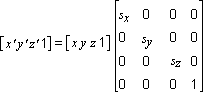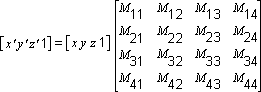
In programs that work with 3D graphics, you can use geometrical transformations to:
·Express the location of an object relative to another object.
·Rotate, shear, and size objects.
·Change viewing positions, directions, and perspective.
You can transform any point into another point by using a 4-by-4 matrix. In the following example, a matrix is used to reinterpret the point (x, y, z), producing the new point (x', y', z'):
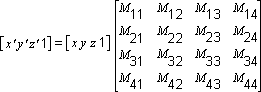
You perform the following operations on (x, y, z) and the matrix to produce the point (x', y', z'):
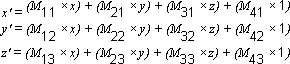
The most common transformations are translation, rotation, and scaling. You can combine the matrices that produce these effects into a single matrix to calculate several transformations at once. For example, you can build a single matrix to translate and rotate a series of points.
Matrices are specified in row order. For example, the following matrix could be represented by an array:
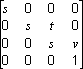
The array for this matrix would look like the following:
D3DMATRIX scale = {
D3DVAL(s), 0, 0, 0,
0, D3DVAL(s), D3DVAL(t), 0,
0, 0, D3DVAL(s), D3DVAL(v),
0, 0, 0, D3DVAL(1)
};
Translation
The following transformation translates the point (x, y, z) to a new point (x', y', z'):
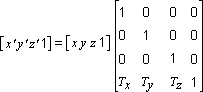
Rotation
The transformations described in this section are for left-handed coordinate systems, and so may be different from transformation matrices you have seen elsewhere.
The following transformation rotates the point (x, y, z) around the x-axis, producing a new point (x', y', z'):
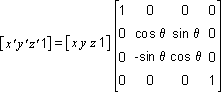
The following transformation rotates the point around the y-axis:
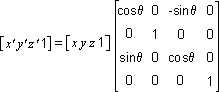
The following transformation rotates the point around the z-axis:
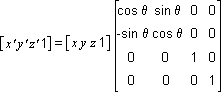
Note that in these example matrices, the Greek letter theta stands for the angle of rotation, specified in radians. Angles are measured clockwise when looking along the rotation axis toward the origin.
Scaling
The following transformation scales the point (x, y, z) by arbitrary values in the x-, y-, and z-directions to a new point (x', y', z'):