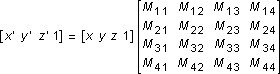
In programs that work with 3D graphics, you can use geometrical transformations to:
·Express the location of an object relative to another object.
·Rotate, shear, and size objects.
·Change viewing positions, directions, and perspective.
You can transform any point into another point by using a 4-by-4 matrix. In the following example, a matrix is used to reinterpret the point (x, y, z), producing the new point (x', y', z'):
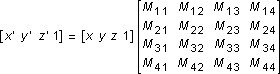
You perform the following operations on (x, y, z) and the matrix to produce the point (x', y', z'):
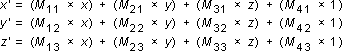
The most common transformations are translation, rotation, and scaling. You can combine the matrices that produce these effects into a single matrix to calculate several transformations at once. For example, you can build a single matrix to translate and rotate a series of points.
Matrices are specified in row order. For example, the following matrix could be represented by an array:

The array for this matrix would look like the following:
D3DMATRIX scale = {
D3DVAL(s), 0, 0, 0,
0, D3DVAL(s), D3DVAL(t), 0,
0, 0, D3DVAL(s), D3DVAL(v),
0, 0, 0, D3DVAL(1)
};
This section describes the 3D transformations available to your applications through Direct3D.
Other parts of this documentation also discuss transformations. You can find a general discussion of transformations in the section devoted to viewports in Retained Mode, Transformations. For a discussion of transformations in frames, see Transformations. Although each of these sections discusses Retained-Mode API, the architecture and mathematics of the transformations apply to both Retained Mode and Immediate Mode. In addition, the "Direct3D Architecture" section includes a section called Transformation Module that discusses the transformation module.