Transformations

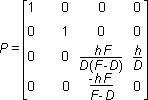
To render objects with 3D coordinates in a 2D window, the object must be transformed into the camera's frame. A projection matrix is then used to give a four-element homogeneous coordinate [x y z w], which is used to derive a three-element coordinate [x/w y/w z/w], where [x/w y/w] is the coordinate to be used in the window and z/w is the depth, ranging from 0 at the front clipping plane to 1 at the back clipping plane. The projection matrix is a combination of a perspective transformation followed by a scaling and translation to scale the objects into the window.

The following matrix is the projection matrix. In these formulas, h is the half-height of the viewing frustum, F is the position in z-coordinates of the back clipping plane, and D is the position in z-coordinates of the front clipping plane:

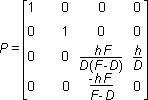
In Direct3D, the 4,4 element of the projection matrix cannot be a negative number.

The following matrix is the window-scaling matrix. (The scales are dependent on the size and position of the window.) In these formulas, s is the window-scaling factor and o is the window origin:

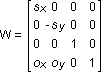
The following matrix is the viewing matrix. This is a combination of the projection matrix and window matrix, or the dot product of P and W:

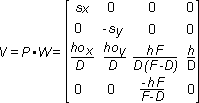
The scaling factors and origin sx, sy, ox, and oy are chosen so that the region [-h -h D] to [h h D] fits exactly into either the window's height or the window's width, whichever is larger.

The application can use the IDirect3DRMViewport::Transform and IDirect3DRMViewport::InverseTransform methods to transform vectors to screen coordinates from world coordinates and vice versa. An application can use these methods to support dragging, as shown in the following example:

/*

* Drag a frame by [delta_x delta_y] pixels in the view.

*/

void DragFrame(LPDIRECT3DRMVIEWPORT view,

LPDIRECT3DRMFRAME frame,

LPDIRECT3DRMFRAME scene,

int delta_x, int delta_y)

{

D3DVECTOR p1;

D3DRMVECTOR4D p2;

frame->GetPosition(scene, &p1);

view->Transform(&p2, &p1);

p2.x += delta_x * p2.w;

p2.y += delta_y * p2.w;

view->InverseTransform(&p1, &p2);

frame->SetPosition(scene, p1.x, p1.y, p1.z);

}

An application uses the viewport transformation to ensure that the distance by which the object is moved in world coordinates is scaled by the object's distance from the camera to account for perspective. Note that the result from IDirect3DRMViewport::Transform is a four-element homogeneous vector. This avoids the problems associated with coordinates being scaled by an infinite amount near the camera's position.

The viewport projection matrix produces a well-defined 3D coordinate only for points inside the viewing frustum. For a homogeneous point [x y z w] after projection, this is true if the following equations hold:

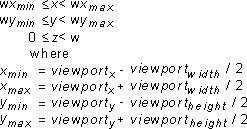
For information about transformations for frames, see Transformations. The "Direct3D Architecture" section includes a section called Transformation Module that discusses the transformation module. For an overview of the mathematics of transformations, see 3D Transformations.