About 3-D Transformations

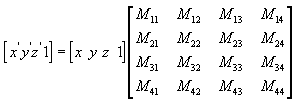
In programs that work with 3-D graphics, you can use geometrical transformations to:

• Express the location of an object relative to another object.
• Rotate and size objects.
• Change viewing positions, directions, and perspectives.

You can transform any point into another point by using a 4×4 matrix. In the following example, a matrix is used to reinterpret the point (x, y, z), producing the new point (x', y', z'):

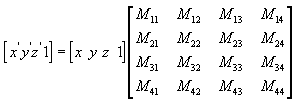
You perform the following operations on (x, y, z) and the matrix to produce the point (x', y', z'):

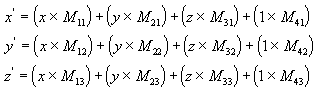
The most common transformations are translation, rotation, and scaling. You can combine the matrices that produce these effects into a single matrix to calculate several transformations at once. For example, you can build a single matrix to translate and rotate a series of points. For more information, see Matrix Concatenation.

Matrices are written in row-column order. A matrix that evenly scales vertices along each axis (known as uniform scaling) is represented by the following matrix (using mathematical notation):

Direct3D Immediate Mode declares matrices as a two dimensional array, using the D3DMATRIX structure. The following example shows how you would initialize a D3DMATRIX structure to act as a uniform scaling matrix:

D3DMATRIX scale = {
    D3DVAL(s),    0,            0,            0,
    0,            D3DVAL(s),    0,            0,
    0,            0,            D3DVAL(s),    0,
    0,            0,            0,            D3DVAL(1)
};