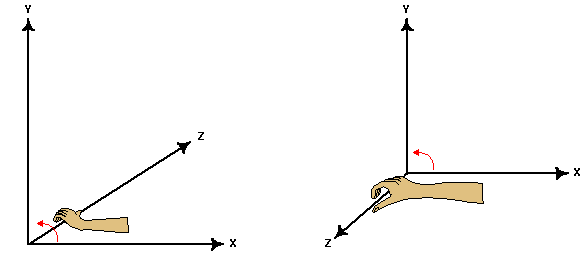
Typically 3-D graphics applications use two types of Cartesian coordinate systems: left-handed and right-handed. In both coordinate systems, the positive x-axis points to the right and the positive y-axis points up. You can remember which direction the positive z-axis points by pointing the fingers of either your left or right hand in the positive x-direction and curling them into the positive y-direction. The direction your thumb points, either toward or away from you, is the direction the positive z-axis points for that coordinate system.

Direct3D uses a left-handed coordinate system. If you are porting an application that relies on right-handedness, you can do so by making two simple changes to the data passed to Direct3D.
It is important to note that there are a wide variety of other coordinate systems used in 3-D software. Left- and right-handed coordinates are the most common. However, it is not unusual for 3-D modeling programs to use a coordinate system in which the y-axis points toward or away from the viewer, and the z-axis points up. In this case, right-handedness is defined as any positive axis (x, y, or z) pointing toward the viewer. Left-handedness is defined as any positive axis (x, y, or z) pointing away from the viewer. If you are porting a left-handed modeling application where the z-axis points up, then in addition to the previous steps you need to do a rotation on all of the vertex data.
The essential operations performed on objects defined in a 3-D coordinate system are translate, rotate, and scale. You can combine these basic transformations to create a transform matrix. For details, see 3-D Transformations.
Remember that when you combine these operations, the results are not commutative—the order in which you multiply matrices is important.