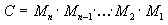
One of the primary advantages of using matrices is that you can combine the effects of two or more matrices by multiplying them. This means that, to rotate a model and then translate it to some location, you don't need to apply two matrices. Instead, you multiply the rotation and translation matrices to produce a composite matrix that contains the whole of their effects. This process often called matrix concatenation, and can be written with the following formula:
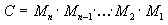
In this formula, C is the composite matrix being created, and M1 through Mn are the individual transformations that matrix C will contain. In most cases, you'll only concatenate two or three matrices, but there is no limit.
(The D3dmath.cpp source file that is included with the DirectX documentation contains the D3DMath_MatrixMultiply helper function to perform matrix multiplication.)
Notice the order in which the matrix multiplication is performed—the order you use is crucial. The preceding formula reflects the right-to-left rule of matrix concatenation. That is, the visible effects of the matrices you use to create a composite matrix occur in right-to-left order. Let's use a typical world transformation matrix as an example. Imagine you were creating the world transformation matrix for a stereotypical "flying saucer." You would probably want to spin the UFO around its center (the y-axis of model space) and translate it to someplace in your scene. To accomplish this effect, you should first create a translation matrix, then multiply it by a rotation matrix, as in the following formula:
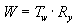
In this formula, Tw is a translation to some position in world coordinates, and Ry is a matrix for rotation about the y-axis.
The order in which you multiply the matrices is important because, unlike multiplying two scalar values, matrix multiplication is not commutative. Multiplying the translate and rotate matrices in the opposite order would have the visual effect of translating the UFO to its world space position, then rotating it around the world origin.
No matter what type of matrix you're trying to create, keep the right-to-left rule in mind to ensure that you achieve the expected effects.