What Is the Projection Transformation?

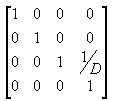
The projection matrix is typically a scale and perspective projection. The projection transformation converts the viewing frustum into a cuboid shape. Because the near end of the viewing frustum is smaller than the far end, this has the effect of expanding objects that are near to the camera; this is how perspective is applied to the scene.

In The Viewing Frustum, the distance between the camera required by the projection transformation and the origin of the space defined by the viewing transformation is defined as D. A beginning for a matrix defining the perspective projection might use this D variable like this:

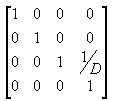
The viewing matrix puts the camera at the origin of the scene. Since the projection matrix needs to have the camera at (0, 0, -D), it translates the vector by -D in the z-direction, by using the following matrix:

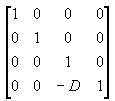
Multiplying these two matrices gives the following composite matrix:

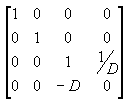
The following illustration shows how the perspective transformation converts a viewing frustum into a new coordinate space. Notice that the frustum becomes cuboid and also that the origin moves from the upper-right corner of the scene to the center.

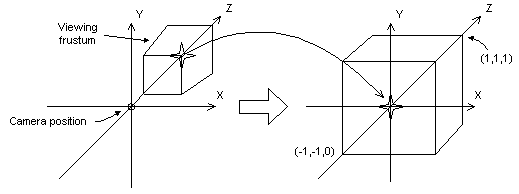
In the perspective transformation, the limits of the x- and y-directions are -1 and 1. The limits of the z-direction are 0 for the front plane and 1 for the back plane.

This matrix translates and scales objects based on a specified distance from the camera to the near clipping plane, but it doesn't consider the field-of-view (fov), and the z-values that it produces for objects in the distance can be nearly identical, making depth comparisons difficult. The following matrix addresses these issues, and adjusts vertices to account for the aspect ratio of the viewport, making it a good choice for the perspective projection:

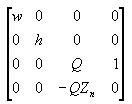
In this matrix, Z_n is the z-value of the near clipping plane. The variables w, h, and Q have the following meanings (noting that fov_w and fov_h represent the viewport's horizontal and vertical fields-of-view, in radians):

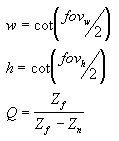
For your application, using field-of-view angles to define the x and y scaling coefficients might not be as convenient as using the viewport's horizontal and vertical dimensions (in camera space). As the math works-out, the following two formulas for w and h use the viewport's dimensions, and are equivalent to the preceding formulas:

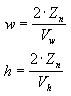
In these formulas, Z_n represents the position of the near clipping plane, and the V_w and V_h variables represent the width and height of the viewport, in camera space. The two dimensions correspond directly to the dwWidth and dwHeight members of the D3DVIEWPORT2 structure.

Whatever formula you decide to use, it's important that you set Z_n to as large a value as you can, as z-values extremely close to the camera don't vary by much, making depth comparisons using 16-bit z-buffers tricky. In Direct3D, the (3,4) element of the projection matrix cannot be a negative number.

As with the world and view transformations, you call the IDirect3DDevice3::SetTransform method to set the projection transformation; for more information, see Setting Transformations.