| DirectX SDK |
One of the primary advantages of using matrices is that you can combine the effects of two or more matrices by multiplying them. This means that, to rotate a model and then translate it to some location, you don't need to apply two matrices. Instead, you multiply the rotation and translation matrices to produce a composite matrix that contains all their effects. This process, called matrix concatenation, can be written with the following formula:
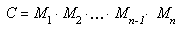
In this formula, C is the composite matrix being created, and M1 through Mn are the individual transformations that matrix C contains. In most cases, only two or three matrices are concatenated, but there is no limit.
C++ applications can use the D3dmath.cpp source file that is included with the DirectX SDK. It contains the D3DMath_MatrixMultiply helper function to perform matrix multiplication. Visual Basic applications can use the MatrixMult subroutine from the Math.bas file that is included with this SDK.
Notice the order in which the matrix multiplication is performed—the order is crucial. The preceding formula reflects the left-to-right rule of matrix concatenation. That is, the visible effects of the matrices that you use to create a composite matrix occur in left-to-right order. A typical world transformation matrix is the following example. Imagine that you are creating the world transformation matrix for a stereotypical flying saucer. You would probably want to spin the UFO around its center (the y-axis of model space) and translate it to some other place in your scene. To accomplish this effect, you would first create a rotation matrix, then multiply it by a translation matrix, as in the following formula:
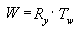
In this formula, Ry is a matrix for rotation about the y-axis, and Tw is a translation to some position in world coordinates.
The order in which you multiply the matrices is important because, unlike multiplying two scalar values, matrix multiplication is not commutative. Multiplying the matrices in the opposite order would have the visual effect of translating the UFO to its world space position, then rotating it around the world origin.
No matter what type of matrix you are creating, remember the left-to-right rule to ensure that you achieve the expected effects.