| DirectX SDK |
The transformations described here are for left-handed coordinate systems, and so may be different from transformation matrices that you have seen elsewhere. For more information, see 3-D Coordinate Systems.
The following transformation rotates the point (x, y, z) around the x-axis, producing a new point (x', y', z')
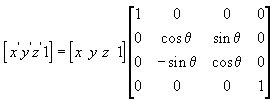
The following transformation rotates the point around the y-axis:
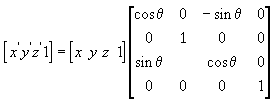
The following transformation rotates the point around the z-axis:
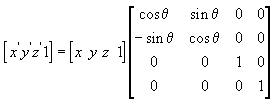
In these example matrices, the Greek letter theta (θ) stands for the angle of rotation, in radians. Angles are measured clockwise when looking along the rotation axis toward the origin.
In a C++ application, use the D3DUtil_SetRotateXMatrix, D3DUtil_SetRotateYMatrix, and D3DUtil_SetRotateZMatrix helper functions in the D3dutil.cpp file to create rotation matrices. (The D3dutil.cpp file is included with this SDK.) The following is the sample code for the D3DUtil_SetRotateXMatrix helper function:
VOID D3DUtil_SetRotateXMatrix( D3DMATRIX& mat, FLOAT fRads )
{
D3DUtil_SetIdentityMatrix( mat );
mat._22 = cosf( fRads );
mat._23 = sinf( fRads );
mat._32 = -sinf( fRads );
mat._33 = cosf( fRads );
}v
Visual Basic applications can use the DirectX7.RotateXMatrix, DirectX7.RotateYMatrix, and DirectX7.RotateZMatrix methods to create rotation matrices.
If you manually created a matrix for rotation about an axis—in this case, the x-axis—the source code would look something like the following:
Sub CreateXRotation(ret As D3DMATRIX, rads As Single)
Dim cosine As Single
Dim sine As Single
cosine = Cos(rads)
sine = Sin(rads)
Call dx.IdentityMatrix(ret) ' Method of the DirectX7 object.
ret.rc22 = cosine
ret.rc23 = sine
ret.rc32 = -sine
ret.rc33 = cosine
End Sub