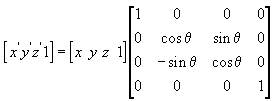
| Microsoft DirectX 8.1 (Visual Basic) |
The transformations described here are for left-handed coordinate systems, and so may be different from transformation matrices that you have seen elsewhere. For more information, see 3-D Coordinate Systems.
The following transformation rotates the point (x, y, z) around the x-axis, producing a new point (x', y', z').
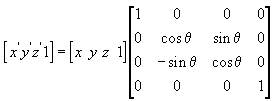
The following transformation rotates the point around the y-axis.
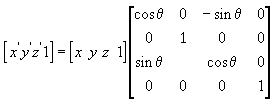
The following transformation rotates the point around the z-axis.
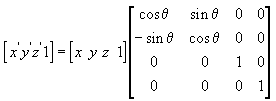
In these example matrices, the Greek letter theta (θ) stands for the angle of rotation, in radians. Angles are measured clockwise when looking along the rotation axis toward the origin.
In a Microsoft® Visual Basic® application, use the D3DXMatrixRotationX, D3DXMatrixRotationY, and D3DXMatrixRotationZ functions supplied by the Direct3DX utility library to create rotation matrices.
If you manually create a matrix for rotation about an axis—in this case, the x-axis—the source code looks something like the following:
Sub CreateXRotation(ret As D3DMATRIX, rads As Single)
Dim cosine As Single
Dim sine As Single
cosine = Cos(rads)
sine = Sin(rads)
D3DXMatrixIdentity ret ' Implemented by Direct3DX.
ret.m22 = cosine
ret.m23 = sine
ret.m32 = -sine
ret.m33 = cosine
End Sub