Some applications translate (or shift) objects drawn in the client area. by calling the SetWorldTransform function to set the appropriate world-space to page-space transformation. The SetWorldTransform function receives a pointer to an XFORM structure containing the appropriate values. The eDx and eDy members of XFORM specify the horizontal and vertical translation components, respectively.
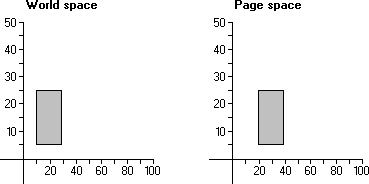
When translation occurs, each point in an object is shifted vertically, horizontally, or both, by a specified amount. The following illustration shows a 20- by 20-unit rectangle that was translated to the right by 10 units when copied from world coordinate space to page coordinate space.

In the preceding illustration, the x-coordinate of each point in the rectangle is 10 units greater than the original x-coordinate.
Horizontal translation can be represented by the following algorithm.
x' = x + Dx
Where x' is the new x-coordinate, x is the original x-coordinate, and Dx is the horizontal distance moved.
Vertical translation can be represented by the following algorithm.
y' = y + Dy
Where y' is the new y-coordinate, y is the original y-coordinate, and Dy is the vertical distance moved.
The horizontal and vertical translation transformations can be combined into a single operation by using a 3-by-3 matrix.
|1 0 0|
|x' y' 1| = |x y 1| * |0 1 0|
|Dx Dy 1|
(The rules of matrix multiplication state that the number of rows in one matrix must equal the number of columns in the other. The integer 1 in the matrix |x y 1| is a placeholder that was added to meet this requirement.)
The 3-by-3 matrix that produced the illustrated translation transformation contains the following values.
|1 0 0|
|0 1 0|
|10 0 1|