Once you understand the target environment, the volume configuration guidelines, and the fault-tolerance requirements the next step is determining how many disks to distribute the data across and which type of disks are required. The goal is to use the lowest cost/megabyte drives, usually the largest drives available, while having enough drives to satisfy the physical I/O rate required by the application. The information presented here will help in meeting this goal.
The number and type of disk drives required by a disk subsystem volume is dependent upon the throughput requirements of the environment and the total amount of data on the server. Throughput requirements are composed of two characteristics, the degree of concurrency among user requests and the request rate from the application. Concurrency and request rate are distinct, but related concepts. Concurrency refers to the number of physical requests that are in the process of being executed by the disk controller(s). The degree of concurrency is primarily influenced by the number of users on the system and the frequency of requests from those users. Request rate is the absolute number of reads and writes per unit of time, usually expressed as I/O's per second. Usually, the higher the concurrency level, the higher the request rate. Yet, fairly high request rates can be generated by a single batch process with no concurrent requests. Of course, the number of physical disk requests that actually occur will depend upon the size of the database relative to the amount of disk cache and the resulting cache hit rate. The worst case scenario would result in as many concurrent disk requests as simultaneous user requests.
The reason for understanding the application I/O request rate is that multiple I/O requests can typically be processed in parallel if the data is distributed across multiple disk drives. Therefore, even though large drives are usually "faster" than smaller drives, this performance difference cannot offset the advantage of two drives' ability to respond to multiple requests in parallel. The target number of drives in a server should be approximately equal to the sustained or average number of simultaneous I/O requests, with three drives being a typical minimum for the data and index files.
The following evaluation process determines the number of drives required by a volume containing data accessed randomly by multiple users. Repeat this process for each volume to be used on a database server. In the case of high transaction rate systems, this process may yield too many drives to fit on a single controller, at which point the drives can be split into multiple, equal volumes across controllers. For systems or volumes using purely sequential I/O or having no concurrent disk requests, i.e. only one or two users on the system at a time, strict calculations for the number of drives is not required. For this case, use the fastest drives available and as many as required to meet the space requirements of the system.
The steps used to determine the optimal number of drives are summarized here followed by a detailed explanation of each step and several case studies:
The first step in calculating the number and size of drives to use is determining the request rate of the application. Without this information it is not possible to make an accurate estimation of the number and type of drives to use. The following equations provide rough estimates to the number of I/O requests generated by an application. Due to optimization routines in the controller to reduce the total I/O requests, these equations do not yield exact loads. They do, however, provide a tool for making conservative comparisons of the load the drives may be required to sustain under alternative RAID configurations. The RAID-5 equation component of (4*writes) implies that each database write incurs 4 physical I/O's, 2 reads and 2 writes; it is not meant to imply 4 physical write operations for each database write operation.
Application I/O Requests per Second =
RAID-0:(reads/transaction writes/transaction ) * transactions/second
RAID-1:(reads/transaction 2*writes/transaction ) * transactions/second
RAID-5:(reads/transaction 4*writes/transaction ) * transactions/second
The next step in the process is determining how many drives are required to support the application's I/O demands. Advertised I/O rates of today's typical 500MB through 2GB drives can exceed 70 I/O's per second. However, these results are achieved with pure saturation testing without regard for request latency. Empirical testing has shown that these same disks sustain between 35 and 45 random database requests per second without incurring costly latency delays. Using this range you can determine the approximate number of physical disks which should be configured on the server and what size those drives can be.
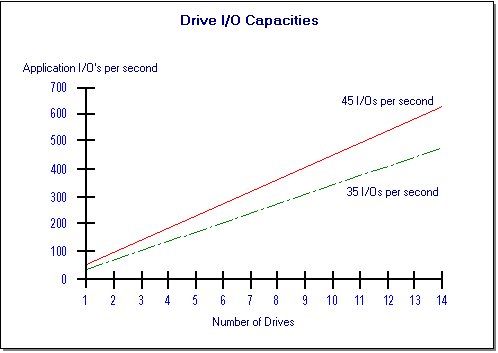
Chart 1 displays two lines which equate to 35 I/O's per second for the lower line and 45 I/O's per second for the upper line. This chart is used in conjunction with the previously discussed equations to determine the number of physical disks required by an application. Locate on the Y-axis the number of I/O's per second required by the application. Move across the graph locating the intersection of the application I/O rate and the 35 to 45 I/O per second area. The number of drives is then determined by locating the drive count on the horizontal axis. The more conservative the implementation desired, the lower the I/O rates per drive that will be required. Also, if using RAID-1 an even number of drives is required. If the result is an odd number of drives, round up to the next even number. When throughput requirements are more than the chart indicates, continue adding controllers and drives until the required throughput is achieved.

Chart 1: SMART Array Drive I/O Rate Capacities
Finally, the total space requirements for the database and support files, combined with the throughput requirements and fault-tolerance, determine the size of disks which will provide an optimal solution. When calculating total space requirements, add an additional 20% free space above the actual data requirements for growth and miscellaneous overhead. Again, a set of equations provide the answer to the appropriate size drive.
Drive size requirements based on total space needs and fault-tolerance:
RAID-0: [total space / number of drives] Rounded up to next drive size
RAID-1: [total space / (number of drives / 2)] Rounded up to next drive size
RAID-5: [total space / (number of drives - number of controller volumes)] Rounded up to next drive size
Several examples are presented which illustrate the use of this process. All RAID levels are presented for each case. Some cases still require a judgment call by the implementor to choose the number of drives or drive sizes, but the alternatives are drastically narrowed. The alternatives chosen are conservative configurations and the reason for the choice, if not a single alternative, is explained.
Case 1: Complex transaction processing system requiring multiple queries per update.
| Reads: | 100/transaction |
| Writes: | 5/transaction |
| Transaction rate: | 2/second |
| Space requirements: | 3GB Database 20% Free space = 3.6GB |
RAID-0:(100 5) * 2 = 205 I/O's / Second
205 I/O's / Second => 5 or 6 Drives
3.6 / 6 = .6 => Round up to next drive size => 1GB Drives
A conservative implementation yields 6 1GB drives for the data volume.
RAID-1:(100 (2*5)) * 2 = 220 I/O's / Second
220 I/O's / Second => 6 or 8 Drives
3.6 / (8 / 2) = .9 => Round up to next drive size => 1GB Drives
A conservative implementation yields 8 1GB drives for the data volume. The alternative of using 6 drives was not chosen due to possibly lower performance and 2GB drives would be required to meet space requirements. Using 2GB drives would yield a higher cost system in addition to lower performance.
RAID-5:(100 (4*5)) * 2 = 240 I/O's / Second
240 I/O's / Second => 6 or 7 Drives
3.6 / (7 - 1) = .6 => Round up to next drive size => 1GB Drives
A conservative implementation yields 7 1GB drives for the data volume.
Case 2: High-end OLTP system with several hundred users and a large database.
| Reads: | 20/transaction |
| Writes: | 8/transaction |
| Transaction rate: | 15/second |
| Space requirements: | 10GB Database 20% Free space = 12GB |
RAID-0:(20 8) * 15 = 420 I/O's / Second
420 I/O's / Second => 10 to 12 Drives
12 / 12 = 1.0 => Round up to next drive size => 1GB Drives
12 1GB drives for the data volume was chosen for this case. As in an earlier example, if 10 drives would have been used, 2GB drives would be required yielding a more expensive, lower performance system. The up side of 2GB drives would have been more available space for growth.
RAID-1:(20 (2*8)) * 15 = 540 I/O's / Second
540 I/O's / Second => 12 to 14 Drives
12 / (14 / 2) = 1.7 => Round up to next drive size => 2GB Drives
14 2GB drives are required for the data volume.
RAID-5:(20 (4*8)) * 15 = 780 I/O's / Second
780 I/O's / Second => 18 to 22 Drives
12 / (22 - 2) = .60 => Round up to next drive size => 1GB Drives
For this system, two controllers with 11 drives each using RAID-5 would be recommended. Notice in this example the value '2' was subtracted from the drive count instead of 1 as used previously. This is required when the drive count exceeds the capacity of a single volume or controller. Each volume will be using n+1 parity, therefore, 1 must be subtracted for each volume to determine usable space.
In this case, due to the very high I/O rates, RAID-1 and RAID-5 have similar costs. The reason is that the RAID-5 implementation requires many drive above the absolute space requirements to achieve acceptable performance levels. The RAID-1 solution, on the other hand, fits the space requirements much closer.
Case 3: Complex decision support with several simultaneous users.
| Reads: | 1000/transaction |
| Writes: | 10/transaction (temporary space for sorting & grouping) |
| Peak transaction rate: | 3/minute or 0.05/second |
| Space requirements: | 5GB Database 20% Free space = 6GB |
RAID-0:(1000 10) * 0.05 = 50.5 I/O's / Second
50.5 I/O's / Second => 2 Drives
6 / 2 = 3 => Largest drive currently available => 2GB Drives
3 2GB drives are required for the data volume due to space requirements.
RAID-1:(1000 (2*10)) * 0.05 = 51 I/O's / Second
51 I/O's / Second => 2 Drives
6 / (2 / 2) = 6 => Largest drive currently available => 2GB Drives
6 2GB drives are required for the data volume due to space requirements.
RAID-5:(1000 (4*10)) * 0.05 = 52 I/O's / Second
52 I/O's / Second => 2 Drives
6 / (2 - 1) = 6 => Largest drive currently available => 2GB Drives
4 2GB drives are required for the data volume due to space requirements.
The general conclusion from this discussion is that more, smaller disks are best for high user, high I/O, high concurrency systems and fewer, larger disks work best for environments with one/few users, high I/O, low concurrency requirements.