Microsoft Corporation
September 10, 1996
Cryptography provides a set of techniques for encoding data and messages such that the data and messages can be stored and transmitted securely. This section introduces the basic terminology of cryptography and explains some of the common methods used.
Cryptography allows a series of operations or actions on data. The two fundamental operations are encryption (with decryption as its inverse) and signing (with verification of signature as its matching operation). Encryption is analogous to enclosing data in an opaque envelope; decryption is analogous to removing it from the envelope. Signature is similar to physically signing a document, and initialing each section to show that no portion of the document has changed. Verification of signature is roughly equivalent to matching the signature to a "signature on file" card, and verifying that no portion of the document has changed. Certificates are signed documents which match public keys to other information.
Public-key cryptography (as opposed to symmetric key cryptography) relies on one-way functions, functions which are easy to calculate but hard to invert or reverse without prior knowledge. One example is factorization: it's often difficult to factor large numbers, but easy to verify a factorization. For example, it's harder to factor 4,399 than to verify that 53*83 = 4,399. Public-key cryptography exploits this asymmetry of effort to create one-way functions: functions where anyone can perform one operation (encryption or verification of signature), but it is extremely difficult to invert the operation (decryption or creation of signature) without having full information.
This is accomplished cryptographically through the use of two related, but different keys—a key pair. These keys are created at the same time. They are mathematically related in that the private key is required to invert operations performed with the public key, and the public key is required to invert operations performed with the private key.
If the public key is widely distributed, and the private key kept private, then there is a many to one function: anyone can use the public key to perform cryptographic operations, but only the person holding the private key can invert it—and a one-to-many function: the person holding the private key can perform an operation, which anyone holding the public key can invert. These two functions are used for encryption (many people can encrypt, only one can decrypt), and signature (only one can sign, many people can verify signature).
Symmetric algorithms are the most common type of encryption algorithm. They are known as symmetric because the same key is used for both encryption and decryption. Unlike the keys used with public-key algorithms, symmetric keys are frequently changed. For this reason, they are referred to here as session keys.
Compared to public-key algorithms, symmetric algorithms are very fast and, thus, are preferred when encrypting large amounts of data. Some of the more common symmetric algorithms are RC4, and the Data Encryption Standard (DES).
Many modern cryptographic protocols use a combination of public-key cryptography and symmetric cryptography to obtain the benefits of both: public-key algorithms to exchange a symmetric key, and symmetric algorithms to quickly encrypt or decrypt data.
Using data encryption, a plaintext message can be encoded so it appears as random gibberish and is very difficult to transform back to the original message without a secret key. (In this document, the term message is used to refer to any piece of data.) This message can consist of ASCII text, a database file, or any data you want to store or transmit securely. Plaintext is used to refer to data that has not been encrypted, while ciphertext refers to data that has.
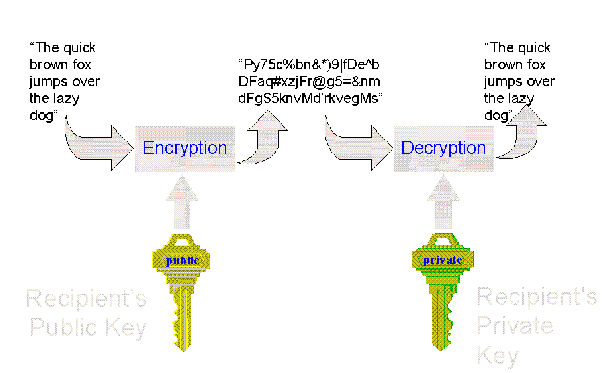
Once a message has been encrypted, it can be stored on nonsecure media or transmitted on an nonsecure network and still remain secret. Later, the message can be decrypted into its original form. This process is shown in the following illustration.

Figure 1. Encryption and decryption using public-key cryptography
When a message is encrypted, an encryption key is used. This is analogous to the physical key that is used to lock a padlock. To decrypt the message, the corresponding decryption key must be used. It is very important to properly restrict access to the decryption key, because anyone who possesses it will be able to decrypt all messages that were encrypted with the matching encryption key.
This may come as a surprise, but data encryption/decryption is pretty straightforward. The really difficult part is keeping the keys safe and transmitting them securely to other users.
Digital signatures can be used when you have a message that you plan to distribute in plaintext form, and you want the recipients to be able to verify that the message comes from you and that it hasn't been tampered with since it left your hands. Signing a message does not alter the message, it simply generates a digital signature string you can bundle with the message or transmit separately.
Digital signatures are generated using public-key signature algorithms. A private key is used to generate the signature, and the corresponding public key is used to validate the signature. This process is shown in the following illustration.
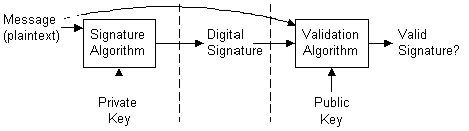
Figure 2. Signature generation/validation process
Digital signatures provide benefits separate from encryption. They allow users to verify that a document came from the holder of a private key and hasn't changed since signature. The document may or may not be encrypted in addition to being signed. (Note: good cryptographic procedure is always to sign before encrypting—that way you know what's being signed. Imagine signing an envelope without knowing what's inside!).
Digital signatures are created by encrypting a hash of the document with a private key. The hash of the document is essentially a miniature fingerprint of the document. The hashing functions used are similar to the hashing functions in use throughout computer science—functions which take a large data input and return a smaller output of fixed size—with a few key distinctions. They should be as "one-way" as possible: if you know the value of a hash (and potentially the original document), it should be very difficult to create another document with the same hash value. It should be especially difficult (ideally impossible) to modify the original document by a character here or there and obtain the same hash value.
A digital signature is hash encrypted with a private signature key. Verifying a digital signature is done by decrypting the signature using the public signature key, and matching the result against a hash of the original document. (Note: good cryptographic procedure recommends using a different key specifically for signature, rather than a general purpose key for both encryption or key exchange and signature.)
The strength of a signature is dependent on the quality of the one-way hash function, and the strength of the encryption of that hash. If the one-way hash function can be subverted, than the original document might be changed. If the encryption isn't sufficiently strong, then the document might have come from someone other than the holder of the private key.
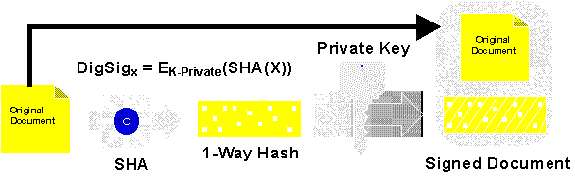
Figure 3. Hashing and signature
So far, we are able to encrypt and decrypt documents, and sign and verify their signatures. Both of these functions require our ability to distribute public keys and match them to the holder of the private key.
This raises the question—how do you know to whom an arbitrary public key belongs? If you received a public key and were told that this was the public key for your bank, would you believe it? One very appropriate answer to this question might be "Who told me?"
Certificates help answer this question. In essence, they are signed documents, which match public keys to other information, such as a name or e-mail address. Certificates are signed by certificate authorities (CAs), who issue certificates. In essence, a certificate authority is a commonly trusted third party, who is relied upon to verify the matching of public keys to identity, e-mail name, or other such information (e.g. issuance of credit, access privileges). Certificate authorities are similar to notaries public.
When two people trust the same CA, by exchanging certificates signed by that CA they can learn each other’s public keys and use them to encrypt and exchange data or verify the signatures on a document.
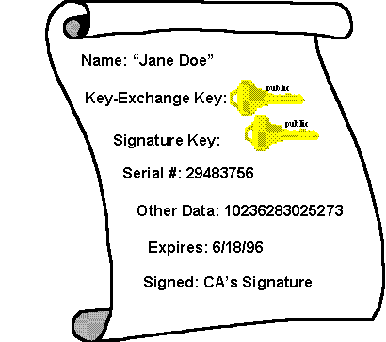
Figure 4. A certificate
Certificate creation is a straightforward process, with six steps:
To verify a certificate, all that is necessary is the public key of the CA (plus a possible check against a revocation list). Certificates and CA's reduce the public-key distribution problem from verifying and trusting one (or more) public keys per individual to verifying and trusting the CA's public key and relying on that to allow verification of others.
Certificate authorities can also certify sub-authorities, who can issue their own certificates. This allows "trees of trust," which, among other things, reduces the burden on a centralized server. For example, imagine a large corporation with four divisions. The main CA would certify four sub-CAs (one per division) which would issue certificates for everyone in each division. Cross-divisional certification works so long as everyone has the public key of the main CA, which it can use to verify the credential of the sub-CA.
Certificates have a limited life. They are requested, created, and then either are revoked (if compromised) or expire. Expiration is important, as advances in computing power and the potential for the discovery of holes in algorithms or protocols may make certificates unreliable. Revocation is important if private keys are compromised or if there has been a change in status or policy (for example, a certificate indicating that TomC is an employee of The Firm should be revoked if he leaves The Firm.).
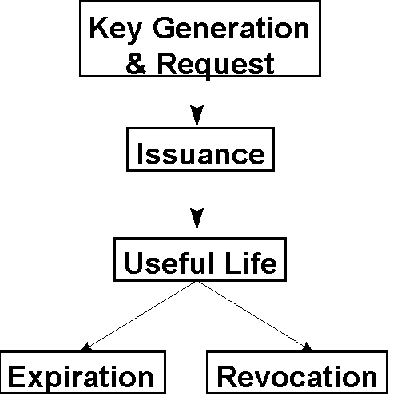
Figure 5. The life of a certificate
Revocation of a certificate uses a Certificate Revocation List (CRL) and is very similar to revocation of a bank card in the physical world. A bank cannot force someone to cut up their bank card—and a CA cannot force destruction of all copies of a certificate. However, in the process of requesting authorization for a purchase above some minimum value, a bank card will be checked against a Card Revocation List to make sure that it is still valid. Someone who is going to use a certificate might want to check against a CRL to ensure validity of the certificate.
A cryptographic protocol is a combination of the basic cryptographic elements of encryption/decryption, hashing, signature, signature verification, certificate issuance, checking and revocation to accomplish some desired goal.
Examples of these include:
The strength of the operations depend on a number of things. All public-key cryptographic operations and protocols require that the private keys be kept private. Here's a summary of some of the additional measures:
As the paragraphs above make clear, cryptography is vulnerable to both increases in computing power and discoveries of weaknesses in algorithms. Cryptography must be easily upgraded or replaced to be most valuable.
For example, Moore's law (computing power doubles every 18 months) shows that a cryptographic algorithm that might take 16,000 years to invert using brute force techniques on a single PC in 1996 might take only 1,000 years to invert on a single PC in 2002. The availability of cycles on networked PCs only exacerbates this situation.
Algorithms which were once thought to be secure may have holes. For example, the MD4 algorithm (a hashing algorithm) was believed to be difficult to subvert but it has been shown to be insecure.
Protocols that relied upon key lengths or hashing algorithms might be fine in themselves, but might be vulnerable because of insufficient key lengths or poor choice of algorithm. Rather than rewriting a protocol or solution from scratch, systems should allow key lengths to be increased or strong algorithms to be substituted when a weakness is found.