NPV

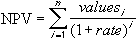
Calculates the net present value of an investment by using a discount rate and a series of future payments (negative values) and income (positive values).

Syntax

NPV(rate,value1,value2, ...)

Rate   is the rate of discount over the length of one period.

Value1,value2, ...   are 1 to 29 arguments representing the payments and income.

• Value1,value2, ... must be equally spaced in time and occur at the end of each period.
• NPV uses the order of value1,value2, ... to interpret the order of cash flows. Be sure to enter your payment and income values in the correct sequence.
• Arguments that are numbers, empty cells, logical values, or text representations of numbers are counted; arguments that are error values or text that cannot be translated into numbers are ignored.
• If an argument is an array or reference, only numbers in that array or reference are counted. Empty cells, logical values, text, or error values in the array or reference are ignored.

Remarks

• The NPV investment begins one period before the date of the value1 cash flow and ends with the last cash flow in the list. The NPV calculation is based on future cash flows. If your first cash flow occurs at the beginning of the first period, the first value must be added to the NPV result, not included in the values arguments. For more information, see the examples below.
• If n is the number of cash flows in the list of values, the formula for NPV is:

  

• NPV is similar to the PV function (present value). The primary difference between PV and NPV is that PV allows cash flows to begin either at the end or at the beginning of the period. Unlike the variable NPV cash flow values, PV cash flows must be constant throughout the investment. For information about annuities and financial functions, see PV.
• NPV is also related to the IRR function (internal rate of return). IRR is the rate for which NPV equals zero: NPV(IRR(...), ...) = 0.

Examples

Suppose you're considering an investment in which you pay $10,000 one year from today and receive an annual income of $3,000, $4,200, and $6,800 in the three years that follow. Assuming an annual discount rate of 10 percent, the net present value of this investment is:

NPV(10%, -10000, 3000, 4200, 6800) equals $1,188.44

In the preceding example, you include the initial $10,000 cost as one of the values, because the payment occurs at the end of the first period.

Consider an investment that starts at the beginning of the first period. Suppose you're interested in buying a shoe store. The cost of the business is $40,000, and you expect to receive the following income for the first five years of operation: $8,000, $9,200, $10,000, $12,000, and $14,500. The annual discount rate is 8 percent. This might represent the rate of inflation or the interest rate of a competing investment.

If the cost and income figures from the shoe store are entered in B1 through B6 respectively, then net present value of the shoe store investment is given by:

NPV(8%, B2:B6)+B1 equals $1,922.06

In the preceding example, you don't include the initial $40,000 cost as one of the values, because the payment occurs at the beginning of the first period.

Suppose your shoe store's roof collapses during the sixth year and you assume a loss of $9000 for that year. The net present value of the shoe store investment after six years is given by:

NPV(8%, B2:B6, -9000)+B1 equals -$3,749.47