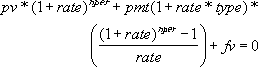
If rate is 0, then:
(pmt * nper) + pv + fv = 0
Returns the present value of an investment. The present value is the total amount that a series of future payments is worth now. For example, when you borrow money, the loan amount is the present value to the lender.
Syntax
PV(rate,nper,pmt,fv,type)
Rate is the interest rate per period. For example, if you obtain an automobile loan at a 10 percent annual interest rate and make monthly payments, your interest rate per month is 10%/12, or 0.83%. You would enter 10%/12, or 0.83%, or 0.0083, into the formula as the rate.
Nper is the total number of payment periods in an annuity. For example, if you get a four-year car loan and make monthly payments, your loan has 4*12 (or 48) periods. You would enter 48 into the formula for nper.
Pmt is the payment made each period and cannot change over the life of the annuity. Typically, pmt includes principal and interest but no other fees or taxes. For example, the monthly payments on a $10,000, four-year car loan at 12 percent are $263.33. You would enter -263.33 into the formula as the pmt.
Fv is the future value, or a cash balance you want to attain after the last payment is made. If fv is omitted, it is assumed to be 0 (the future value of a loan, for example, is 0). For example, if you want to save $50,000 to pay for a special project in 18 years, then $50,000 is the future value. You could then make a conservative guess at an interest rate and determine how much you must save each month.
Type is the number 0 or 1 and indicates when payments are due.
|
Set type equal to |
If payments are due | |
|
0 or omitted |
At the end of the period | |
|
1 |
At the beginning of the period | |
Remarks
|
CUMIPMT |
PPMT |
|
CUMPRINC |
PV |
|
FV |
RATE |
|
FVSCHEDULE |
XIRR |
|
IPMT |
XNPV |
|
PMT |
An annuity is a series of constant cash payments made over a continuous period. For example, a car loan or a mortgage is an annuity. For more information, see the description for each annuity function.
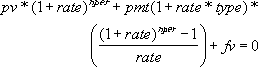
If rate is 0, then:
(pmt * nper) + pv + fv = 0
Example
Suppose you're thinking of buying an insurance annuity that pays $500 at the end of every month for the next 20 years. The cost of the annuity is $60,000, and the money paid out will earn 8 percent. You want to determine whether this would be a good investment. Using the PV function, you find that the present value of the annuity is:
PV(0.08/12, 12*20, 500, , 0) equals -$59,777.15
The result is negative because it represents money that you would pay, an outgoing cash flow. The present value of the annuity ($59,777.15) is less than what you are asked to pay ($60,000). Therefore, you determine this would not be a good investment.