Ruediger R. Asche
Microsoft Developer Network Technology Group
Created: January 6, 1994
Revised: March 11, 1994
Added seven paragraphs on the subtleties of synchronization objects to the section "Synchronization Objects."
This article complements the "Detecting Deadlocks in Multithreaded Win32 Applications" and "The Implementation of DLDETECT.EXE" articles in the Microsoft® Development Library. It describes a constructive process for rewriting a multithreaded application as a Petri net that can be fed into DLDETECT.EXE to derive the formal properties of the application.
triptych, n. 1. Fine arts. A set of three panels or compartments side by side, bearing pictures, carvings, or the like. 2. A hinged, three-leaved tablet, written on, in ancient times, with a stylus. 3. A series of three articles written by Ruediger Asche that cross-reference each other constantly and of which none makes any sense unless read along with the other ones.
(loosely adapted from The Random House Dictionary of the English Language)
So you have read "Detecting Deadlocks in Multithreaded Win32 Applications," a fairly abstract pamphlet about social injustice in the computer world. And, slightly amused, you have looked at the illustrations in "The Implementation of DLDETECT.EXE," a description of a cute little toy that allows you to generate pictures on the screen that look remotely like the construction plan for Gaudi's "Sagrada Familia." And maybe you have wondered, "What the heck is this all about?"
This article is intended to be the missing link. It will enable you to rewrite your multithreaded application as a Petri net (remember the term from "Detecting Deadlocks. . ."?), which you can then type into DLDETECT.EXE to at the very least get a better understanding of the dynamic behavior of your application and possibly help you detect and eliminate deadlock or race conditions in the application.
The first section discusses the synchronization mechanisms of the Win32® Application Programming Interface (API) in terms of Petri subnets, as well as the subtleties of their semantics. (You might want to refer to the article "Multithreading for Rookies" for details.) In the second section, I describe how the toolbox introduced in the first section can be used to rewrite applications as Petri nets. The third section then explains to what extent the Petri nets obtained in the second section can be used to get a better understanding of the properties of a multithreaded application.
Let us look at a single-threaded application first. As I already mentioned in the article "Detecting Deadlocks in Multithreaded Win32 Applications," it would be a perfectly valid technique to rewrite a single-threaded application into a Petri net by simply depicting each program statement as a transition and everything in between as a place. (Remember, places roughly depict "states" that an application can be in, whereas transitions can be interpreted as "actions that transform an application from one state into the other.") Let us look at the following single-threaded application:
void main(void)
{
printf ("Hello World!");
}
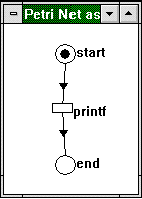
On a very coarse level, we could interpret this application to have two states: one initial state and one final state. The printf statement transforms the application from one state to the other:

Figure 1. The black dot or marking indicates where the program executes initially.
As you can see, all of the Petri nets and net fragments are cut and pasted from DLDETECT screen shots. Wouldn't it be great to have the application be an OLE server so that the respective nets could be activated in place by double-clicking them? (I'll have to put that in the feature list!)
Note that we could go into any arbitrary detail here: The printf statement is not atomic, of course; on the assembly language level, we would probably end up with several dozen statements that are being executed before the application terminates, including all the startup code that the application is linked against.
The point here is that all of those statements are totally irrelevant. As we have seen in "Detecting Deadlocks in Multithreaded Win32 Applications," the only statements we are concerned with in a liveness analysis are synchronization statements and, possibly, control flow statements. In order to get a good understanding of your multithreaded application, I strongly suggest that when analyzing the application, you simply ignore all statements that are not concerned with synchronization. All variable assignments, run-time calls, arithmetic operations, and so forth are most probably totally irrelevant for a liveness discussion; all we are generally concerned with are statements that may suspend a thread.
Let us look at a slightly more interesting version of the "Hello World" application:
void main(void)
{
while (TRUE)
printf ("Hello World!");
}
This may look phony, but in practice, many threads are implemented as infinite loops, performing some kind of background service processing. Figure 2 shows how the whole thing looks as a Petri net.
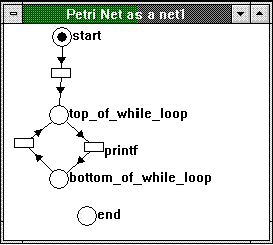
Figure 2. An infinite loop as a Petri net
Obviously, there is no arrow going to the "end" place because the loop is infinite. Here is a version of "Hello World" that features finite iteration.
void main(void)
{ int i = 10;
while (i > 0)
{
printf ("Hello World!");
i--;
};
}
Figure 3 shows how this translates into a Petri net.
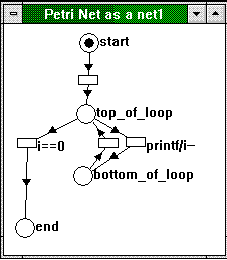
Figure 3. A finite loop as a Petri net
Note that the net does not tell us under what conditions the top_of_loop place takes the "printf/i--" or the "i==0" branch. Although we could theoretically incorporate into the net the information that the loop will be taken ten times, it is generally sufficient to indicate that either transition can be taken. The time at which one or the other statement executes is up to the interpretation of the transition; all the net implies is that when the application has reached the state that is symbolized by the top_of_loop place, it has a choice of taking either transition and may take exactly one of the two, but not both.
So far, this is no big deal. If we determined the net invariants of the above nets, we would find that in all nets there is only one invariant, namely, that the sum of the marks in all places is exactly one at all times. This is no big surprise because a single-threaded application is characterized by the fact that the execution path is always at exactly one point somewhere in the thread, which is another way of expressing the invariant. By the way, in Petri net theory, each subset of places that will never "lose" a mark once there is one in it is called a trap.
Single-threaded applications are not very interesting when it comes to Petri net analyses, so let us add another thread to the application. I will leave out the details here for clarity's sake; the CreateThread call is, in fact, more complex, as you probably know, but I don't have any doubts that you could easily fill in the missing pieces.
long WINAPI ThreadFn(long)
{int i = 10;
while (i>0)
{ printf ("Hello other world!");
i--;
};
}
void main(void)
{ int i = 10;
CloseHandle(CreateThread(...ThreadFn...));
while (i > 0)
{
printf ("Hello World!");
i--;
};
}
Now here is how it starts to become interesting. Figure 4 shows how this looks as a Petri net:
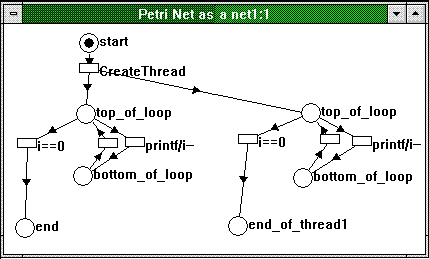
Figure 4. Two threads as a Petri net
We have two almost identical subnets. Once the main thread passes the CreateThread call, a mark will have been put in each of the two top_of_loop places, and that is where the two threads start to execute asynchronously; no relationship between the statements that the threads execute respectively can be made. At any point, an arbitrary firing sequence can put the first thread in any state in its subnet and the other one at any point in its subnet.
If we now choose to view this net as a matrix and select "Find net invariants" from the Matrix menu of DLDETECT.EXE, we see the result shown in Figure 5. (Please refer to the article "Detecting Deadlocks in Multithreaded Win32 Applications" for details on how to interpret an invariant matrix.)
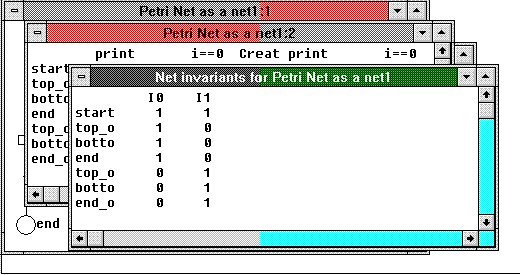
Figure 5. A sample invariant matrix
The first invariant (I0) indicates that Thread 0 is always somewhere in its code, as before, and the other invariant implies that either Thread 0 has not passed its CreateThread statement yet, or Thread 1 is somewhere in its code.
In practice, any multithreaded application will employ some form of synchronization. For example, in the above application, if Thread 0 finishes its computation before Thread 1, the operating system will most likely destroy the process before Thread 1 finishes and may, therefore, leave the computation in Thread 1 in an undefined state. How about waiting for the thread to finish to avoid this?
long WINAPI ThreadFn(long)
{int i = 10;
while (i>0)
{ printf ("Hello other world!");
i--;
};
}
void main(void)
{ int i = 10;
HANDLE hThread;
hThread = CreateThread(...ThreadFn...);
while (i > 0)
{
printf ("Hello World!");
i--;
};
WaitForSingleObject(hThread,INFINTE);
CloseHandle(hThread);
}
Figure 6 shows the same thing as a Petri net, as expected.
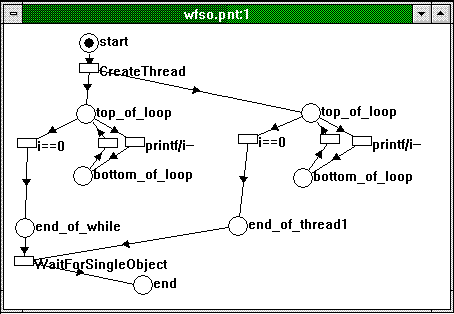
Figure 6. Two synchronized threads as a Petri net
We see here that the transition labeled WaitForSingleObject will only be taken if both threads have reached the end of their respective while statements (that is, both places labeled "end_of_..." are marked).
Let us quickly look at the invariants for this net:

Figure 7. Invariants for the net in Figure 6
This looks quite different from the invariant set in the last example! What I1 (and its counterpart, the linear combination I0+I1) tells us is that Thread 0 has not spawned the secondary thread yet, or has completed the wait, or is lingering somewhere in its while code; the same thing holds for the other thread. I0 tells us that whenever there is a mark in Thread 0's while loop, there must also be one in Thread 1's while loop. This indicates that whenever Thread 0 has finished, Thread 1 must also have terminated its while loop. Thus, we have proven that the synchronization of Thread 0 with Thread 1 has worked!
Now that we have looked at the basics of Petri net philosophy, let us put together a toolbox of small Petri nets that describe the interactions between threads.
As we have seen, any thread, when viewed as a Petri net, basically looks like a linear sequence of places and transitions. Although there may be a scenario in which a place in one thread has a choice between two or more transitions, as we have seen, in each subnet that represents a thread, it can never happen that more than one mark is in the net or that a mark disappears (unless the thread terminates). In terms of net invariants, this can easily be verified by ensuring that one invariant reading "the sum of all marks in all places that represent a thread is always constant" must be found in the invariant set (either explicitly or as a linear combination of other invariants).
Furthermore, each thread has a starting place and an ending place. The ending place may never be reached (if the thread contains an infinite loop), and the starting place of an application's primary thread is always initially marked by definition, whereas it will be initially empty for secondary threads. The subnet in Figure 8 symbolizes a CreateThread statement.
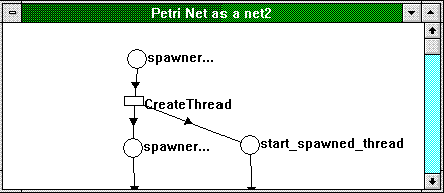
Figure 8. CreateThread as a Petri net
Note that a subnet like this can never be found in a single thread because a single thread can never have more than one mark in any one of its places.
The interesting part is when it comes to synchronization. Recall that a deadlock always implies a condition under which two or more threads become suspended. All the API calls that may suspend a thread are listed below:
Let us look at each of these in turn. WaitForSingleObject (hereafter also referred to as WFSO) looks surprisingly simple in terms of a Petri net, as shown in Figure 9.
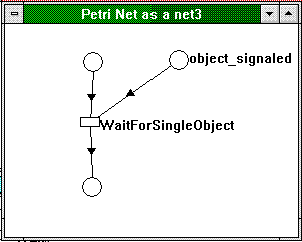
Figure 9. WaitForSingleObject as a Petri net
What it means for an object to be in the signaled state varies, though. For threads, this is easy; the thread attains a signaled state once its "end" place is marked. Watch out, though; there is one subtle problem: Once a thread attains the signaled state, it will always have that state. This is not reflected in our earlier depiction of the two-thread application, where the mark in the thread's end place will be lost in order to satisfy the wait. If there are several threads waiting for the same thread handle, you can use either of the two techniques shown in Figure 10 to depict this in a Petri net.
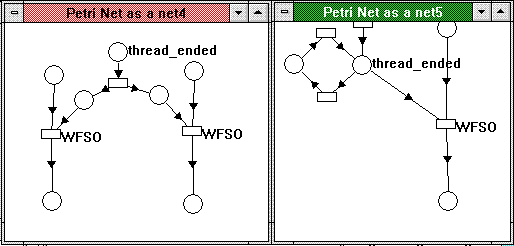
Figure 10. Several calls to WaitForSingleObject on the same handle
In the solution on the left, the thread clones its signaled condition into two places that can be used by two WaitForSingleObject calls, respectively. In the second solution (which is more correct as far as simulating the "real" behavior of WaitForSingleObject is concerned), we add a trap to the thread_ended place; that is, we make sure that as soon as there is a mark in the aforementioned place, the marking can always be regenerated. This way, the same place can serve as many waits as desired.
How about a call to WaitForSingleObject with a time-out, though? That's easy:
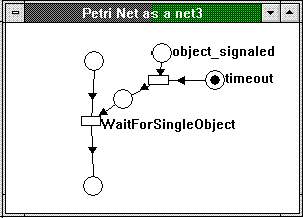
Figure 11. WaitForSingleObject with a time-out
If we analyze the behavior of the Petri net in Figure 11, we find that the behavior looks the same as if the wait were not there. And, in fact, any finite time-out will not deadlock. Just as in the earlier example with the finite iteration, Petri nets don't worry about programmatic details; they are used to make general statements about synchronization conditions in multithreaded applications.
WaitForMultipleObjects (or WFMO) is one of my favorite functions in the Win32 API. It is a real home run because of its beautiful semantics; too bad for OS/2® that it does not have anything similar. Figure 12 shows WaitForMultipleObjects waiting for any object first (that is, a wait that will return if any of the specified objects signals).
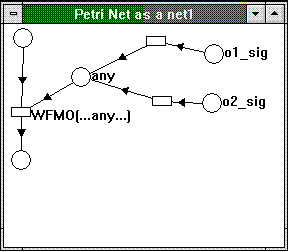
Figure 12. WaitForMultipleObjects waiting for any of its objects
In this case, the blocked thread waits for either of two objects, o1 or o2. As soon as any of the objects attains the signaled state, it can leave a mark in the place labeled, any of which can in turn satisfy the wait. I leave it as an exercise to you to add a time-out option to this net. . .
The reason I like WaitForMultipleObjects so much is that it comes in a second flavor, which is WAIT_FOR_ALL. When you use it in that variation, the function will not return until ALL specified objects have signaled, and those objects that will be unsignaled automatically as soon as the wait is satisfied will become unsignaled atomically. We will see later on why this is really cool. It also looks fairly straightforward as a Petri net:
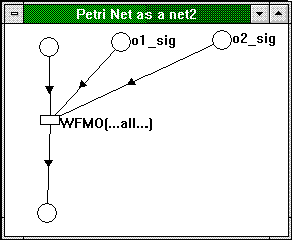
Figure 13. WaitForMultipleObjects waiting for all objects
The WFMO transition will be taken only if the thread is executing it (indicated by a mark in the place leading into the WFMO transition) and all waiting objects are signaled, just as we expected.
The cool thing about rewriting synchronization primitives as Petri nets is that this process gives us a much clearer idea of how they work. Let's first look at mutexes and critical sections, whose semantics are identical, as Figure 14 illustrates.
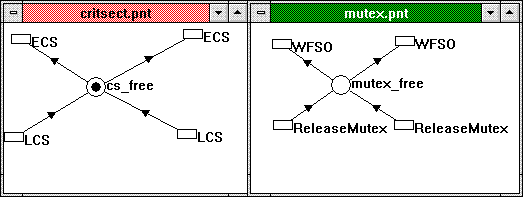
Figure 14. Critical sections and mutexes
As long as the object is unowned, there is a mark in the place that represents it, and any thread that claims the object will remove the mark, thereby blocking other threads that also have a transition relying on that object. (The call that claims the object is represented by ECS for EnterCriticalSection or WFSO for WaitForSingleObject transitions, respectively—of course, WFSO could also read WaitForMultipleObjects.) As long as one thread executes code between a call to claim and a call to release the object (releasing is indicated by LCS for LeaveCriticalSection or ReleaseMutex), it is said to own the critical section or mutex. By keeping track of the ownership of synchronization objects, DLDETECT.EXE could build the resource allocation graph (RAG)—if this feature were implemented—and thereby determine whether the application has deadlocked (as explained in "Detecting Deadlocks in Multithreaded Win32 Applications"). Note that a critical section by definition is unowned when it is created (thus, the mark on the place representing the critical section), whereas a mutex can be assigned initial ownership.
This is the easy way to model critical sections and semaphores, and in the first version of the article, that is how I left off. Since then I have learned that there is no such thing as "an easy way," and we will have to spend some more time looking at the subtleties of synchronization objects.
Would you think it possible for a thread to deadlock itself? You bet. Take a semaphore object with count 1. (We will look at semaphores right after this discussion). One thread claims the semaphore with a call to WaitForSingleObject. What happens if the same thread tries to claim the same semaphore again? Well, the semaphore is already claimed, and the thread will deadlock itself. In this case, we are hopelessly lost, but generally, semaphores will have a count greater than 1, and another thread will be able to release the semaphore, and therefore, wake up the blocked thread again. This behavior is absolutely consistent with our model.
The way we've modeled critical sections and mutexes so far corresponds pretty much to the definition of mutexes under POSIX, where it is possible for a thread to deadlock itself while waiting for a mutex that it owns. Under the Win32 API, any thread can claim a mutex or a critical section an arbitrary number of times without blocking, but it must release the object as many times as it claimed it before another waiting thread can be awakened. That is, a mutex or critical section object behaves much like an “inverse semaphore” with an infinite (negative) count.
This is, indeed, very troublesome for Petri net modeling. If we were to incorporate this behavior in a Petri net, we would not only need to “link” all instances of one thread trying to claim the same object together, but we would also need to keep track of the number of times a synchronization object has been claimed by the same thread. As I will explain shortly, I restricted the Petri net model to only so-called “1-conservative” nets, which, in effect, makes it impossible to keep track of an arbitrary number of calls to claim a critical section.
I must admit that this behavior sort of blows the formalism out of the water. While it would be possible to assign “ownership” of a mutex or critical section to a thread in a Petri net (which would be a nice feature anyway in order to build the Resource Allocation Graph), the other issue—keeping track of multiple claims—is very hard to model in the formalism “as is.” One would either have to abandon the limitation to "1-conservative" nets or artificially restrict the number of possible nested calls so that a “static” subnet could be used to store at most that number of markings.
You should analyze your application to see whether multiple calls to claim the same synchronization object from within the same thread can occur, and if so, consider this case separately.
The only thing I can say in defense of my formalism is that modeling critical sections and mutexes the way I did is more rigorous than if I had modeled them the way the Win32 API defines them; that is, the formalism might detect a deadlock where there is none, and it would be easy to rule out such a case—but in any case, you are now alerted to that peculiar possibility.
Semaphores are really easy to model in an unrestricted Petri net, that is, a Petri net in which places can be assigned arbitrary capacities. All we would need to do is take the net for a mutex variable, fill it with as many marks as the semaphore can count, and specify that each WaitForSingleObject transition removes one mark from the place and each ReleaseSemaphore transition puts one mark into that place. That would exactly model a semaphore.
Unfortunately, unrestricted Petri nets are difficult to work with because their incidence matrices may contain arbitrary integer values, thereby making it difficult to compute the integer solutions for the null space. Therefore, I restricted the model to so-called "1-conservative" nets in which no place is allowed to have more than one mark. This makes semaphores a little bit awkward to model, but can be done: Figure 15 shows a sample for a semaphore created with count 4.
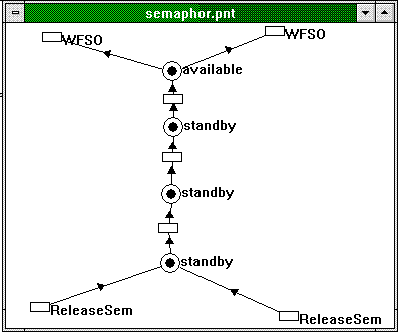
Figure 15. A semaphore with count 4
I have added three places labeled "standby" in Figure 15. The standby and available places should always add up to the semaphore count.
Now for events. Events are weird because there is no notion of ownership; every thread that has access to the event can arbitrarily set or reset it. This is not too difficult to model, but it is really hard to figure out whether events can become involved in a deadlock—for all owned objects (that is, critical sections, mutexes, and semaphores), we can determine who owns the object and, therefore, whose responsibility it is to reclaim the object. A thread that has reset an event may very well become blocked without affecting the liveness of the application (for instance, if another thread decides to signal the event); and likewise, in a deadlocking situation, there might be a thread in the system that could break the deadlock, but we don't know which one. For this reason, events should be used with caution.
Figure 16 shows what events look like.
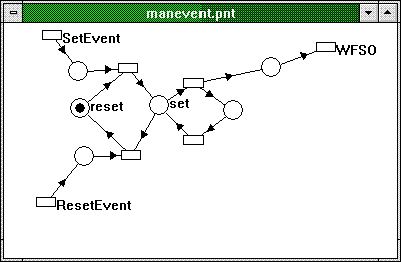
Figure 16. Manual-reset events
Figure 16 illustrates a manual-reset event, that is, an event that gets set and reset manually. The heart of the net here is two small subnets that look like flip-flops: one that acts as a trap such that a mark in the set place will not get lost and one that toggles between the set and reset state, depending on whether the ResetEvent or SetEvent transition is being taken.
The other flavor of event is an auto-reset event that will toggle between the set and reset state automatically once a wait has been satisfied, as shown in Figure 17.
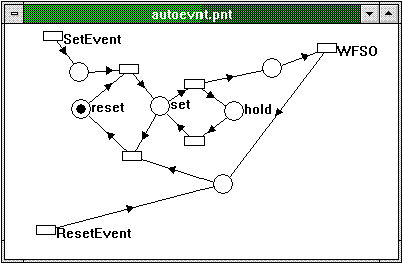
Figure 17. Auto-reset events
Note that in either case, the event can be initially created as set or reset, that is, the mark can be either on the reset or set place. In the examples in Figures 16 and 17, I assumed that the event was initially reset. Only one invariant exists for both types of events, which is that the sum of marks in the set, reset, and hold places is always constant. This verifies the correctness of the net because an event is always either set or reset, so if we lost a mark in that subnet, we would not model an event correctly.
The only remaining Win32 API call that can implicitly suspend a thread is SendMessage. In order to be compatible with the 16-bit Microsoft® Windows™ messaging model, a call to SendMessage will not return before the message is entirely processed. The implementation is slightly different under Win32 than under 16-bit Windows, though; because all applications under Windows 3.1 reside in the same address space, the function is called immediately, whereas under Win32, the sending thread becomes suspended until the receiving thread has picked up a copy of the message and processed it. Consequently, a call to SendMessage may deadlock two threads if the receiver tries to claim a critical resource that the sender owns.
Window functions are somewhat awkward to model, and in most cases, there is really no need to do so. However, in the case of a potential SendMessage deadlock, we should try to model the window function as simply as possible. There is a lot of room for creativity left here, and if you, dear reader, have a good idea on how to do it, please let us know.
Figure 18 shows my suggestion on how to do it.
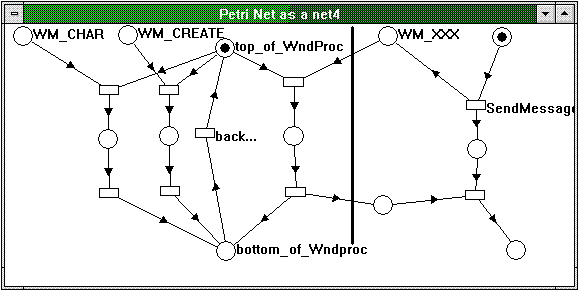
Figure 18. A window function as a Petri net
The bonsai-like creation on the left side of the thick line depicts the window function. Let us assume that the window only processes three messages: WM_CHAR, WM_CREATE, and an application-supplied WM_XXX message (typically, explicitly sent messages are application-supplied). Depending on whether there is a mark in the WM_CHAR, WM_CREATE, or WM_XXX place, the corresponding branch of the window function is taken, and after the message is processed, the "back" transition brings us back to the front.
On the right side of the thick line, the other thread is ready to send the message (indicated by the mark in its uppermost place). When it sends the message, the thread leaves a mark in both the WM_XXX and its successor place (which roughly represents the state "waiting for SendMessage to return"). That place, however, can only take the transition to the next place if the final transition of the window procedure branch that processes WM_XXX has fired.
This closes our toolbox for Petri nets. There are more subtle issues that are worth writing about, such as the impossibility of incorporating SuspendThread and ResumeThread into the Petri net framework. But if you need to use those APIs, you probably know what you are doing anyway. Once more, if you end up actually using this framework and come across other issues that are worth discussing, please let me know.
In the following section, we will have a look at how to put the foregoing discussion into practice.
Let's look at one of the real-life problems that researchers traditionally use to model concurrent problems: The Dining Philosophers. Three philosophers sit around a round table. Each one has a fork to his right, so there are three forks total. However, each philosopher needs two forks to eat. Each philosopher constantly switches between eating and thinking—initially, all philosophers think, and in order to switch to eating with two forks, a philosopher must pick up both the fork to his left (thereby blocking his left comrade from eating) and to his right (thereby preventing his right colleague from eating). If one (or both) of the forks is in use by another philosopher, the philosopher has to wait.
The problem here is how to have a multithreaded application model the scenario correctly. Unrealistic as this problem looks, it has kept computer people busy for ages and probably will do so until doomsday. Let us look at one way of implementing this using the Win32 API:
#include <stdio.h>
#include <windows.h>
typedef struct
{ int iID;
HANDLE hMyObjects[2];
} THREADCONTROLBLOCK, *PTHREADCONTROLBLOCK;
long WINAPI ThreadRoutine(long lParam)
{ PTHREADCONTROLBLOCK pcb=(PTHREADCONTROLBLOCK)lParam;
while (TRUE)
{WaitForSingleObject(pcb->hMyObjects[0],INFINITE);
WaitForSingleObject(pcb->hMyObjects[1],INFINITE);
printf("Eating: Philosopher %d",pcb->iID);
ReleaseMutex(pcb->hMyObjects[1]);
ReleaseMutex(pcb->hMyObjects[0]);
};
return (0);
}
main()
{
HANDLE hMutex1,hMutex2,hMutex3;
THREADCONTROLBLOCK tcb1,tcb2,tcb3;
int iThreadID;
//
hMutex1=CreateMutex(NULL,FALSE,NULL); // Not owned
hMutex2=CreateMutex(NULL,FALSE,NULL);
hMutex3=CreateMutex(NULL,FALSE,NULL);
//
tcb1.iID=1;
tcb1.hMyObjects[0]=hMutex1;
tcb1.hMyObjects[1]=hMutex2;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb1,0,&iThreadID));
tcb2.iID=2;
tcb2.hMyObjects[0]=hMutex2;
tcb2.hMyObjects[1]=hMutex3;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb2,0,&iThreadID));
tcb3.iID=3;
tcb3.hMyObjects[0]=hMutex3;
tcb3.hMyObjects[1]=hMutex1;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb3,0,&iThreadID));
while(TRUE);
return(0);
}
Each philosopher is represented by a thread that performs an infinite loop that toggles between eating and thinking, and each fork is represented by a mutex. Using our toolbox, we can rewrite this into a Petri net, which looks really adventurous, as you can see in Figure 19. (This awesome piece of art can also be found in the source code for the DLDETECT.EXE sample; look for DEADPHIL.PNT.)
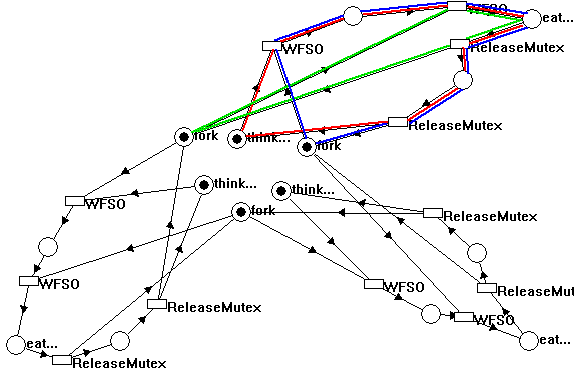
Figure 19. The Dining Philosophers, Museum of Abstract Art, Ruediger Asche, 1994. Medium: Pixel on screen.
In order to make Figure 19 more readable, I have outlined the subnets that represent one of the threads with red and two of the subnets that represent the mutexes with green and blue, respectively. Let us look at the invariants in Figure 20.
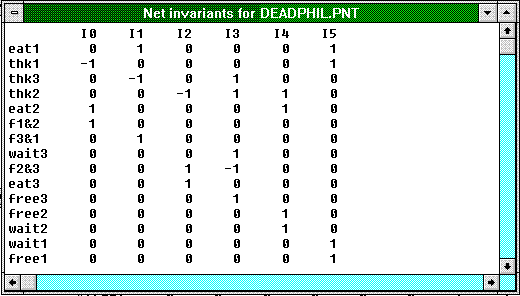
Figure 20. Net invariants for the Dining Philosophers' Petri net
Invariants 4 and 5 (and invariants 2 and 3) tell us reassuringly that each thread is a trap, so we will never lose a mark in a thread (or, in other words, the subnets correctly model the three threads as infinite loops).
Note that the application is set up such that each philosopher first picks up the fork to his left and then the one to his right, and when he is finished eating, he puts back the fork to his right and then to his left. This is reflected in invariants 0, 1, and 2: If a fork is taken, it is implied that the philosopher who sits left of that fork must be eating (because he picks up the fork only if he has grabbed his other one already) and that the philosopher who sits on the other side of that fork must be thinking (because he wasn't fast enough to grab the fork).
Invariant 3 and its symmetric counterparts basically say that if a particular philosopher is not eating (that is, she is either thinking, waiting for one fork, or is about to put back the second fork), then the philosopher to her right is in the thinking state if the fork between them is on the table. This follows directly from the stipulation that a philosopher picks up the fork to her left first and then to her right. This leads us to the interesting question of what happens if all philosophers pick up the fork to their left at the same time. You probably guessed it: The table deadlocks because everybody is waiting for the fork to her right while holding on to the one on her left. Bummer! (In following this problem, you must suspend your disbelief for a while and assume that the philosophers are too inflexible, too stubborn, too dumb, or all of the above to voluntarily relinquish one of their forks, let alone eat with one fork—which is why certain circles like to use three chopsticks in this problem instead of forks.)
Indeed, if we were to simulate a control flow (that is, if the feature were implemented in DLDETECT), we would see the marking shown in Figure 21, from which the net will not recuperate.
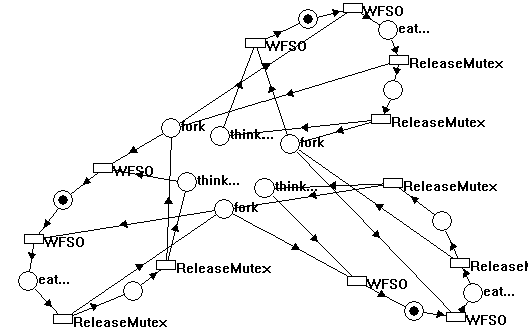
Figure 21. Philosophers not being able to cope with reality
And if we built the resource allocation graph for this scenario, we would see that it contains a circle and, therefore, indeed describes a deadlock.
Several possibilities exist to relieve this problem: We could make the philosophers smarter so that they could time-out with only one fork in their hand, or we could make them pick up and put back the forks in another (not first-in, last-out) order, possibly a random, undefined order. Or we could use the WaitForMultipleObjects solution: Have the philosophers grab both forks at the same time.
Here is the latter solution as a program. Note that it looks almost the same as the former one, except that both forks are claimed at the same time instead of sequentially:
#include <stdio.h>
#include <windows.h>
typedef struct
{ int iID;
HANDLE hMyObjects[2];
} THREADCONTROLBLOCK, *PTHREADCONTROLBLOCK;
long WINAPI ThreadRoutine(long lParam)
{ PTHREADCONTROLBLOCK pcb=(PTHREADCONTROLBLOCK)lParam;
while (TRUE)
{WaitForMultipleObjects(2,pcb->hMyObjects,TRUE,INFINITE);
printf("Eating: Philosopher %d",pcb->iID);
ReleaseMutex(pcb->hMyObjects[1]);
ReleaseMutex(pcb->hMyObjects[0]);
};
return (0);
}
main()
{
HANDLE hMutex1,hMutex2,hMutex3;
THREADCONTROLBLOCK tcb1,tcb2,tcb3;
int iThreadID;
//
hMutex1=CreateMutex(NULL,FALSE,NULL); // Not owned
hMutex2=CreateMutex(NULL,FALSE,NULL);
hMutex3=CreateMutex(NULL,FALSE,NULL);
//
tcb1.iID=1;
tcb1.hMyObjects[0]=hMutex1;
tcb1.hMyObjects[1]=hMutex2;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb1,0,&iThreadID));
tcb2.iID=2;
tcb2.hMyObjects[0]=hMutex2;
tcb2.hMyObjects[1]=hMutex3;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb2,0,&iThreadID));
tcb3.iID=3;
tcb3.hMyObjects[0]=hMutex3;
tcb3.hMyObjects[1]=hMutex1;
CloseHandle(CreateThread(NULL,0,(LPTHREAD_START_ROUTINE)ThreadRoutine,
(void *)&tcb3,0,&iThreadID));
while(TRUE);
return(0);
}
Figure 22 describes the same thing as a Petri net (I also provide the net with the source code as DINPHIL.PNT):
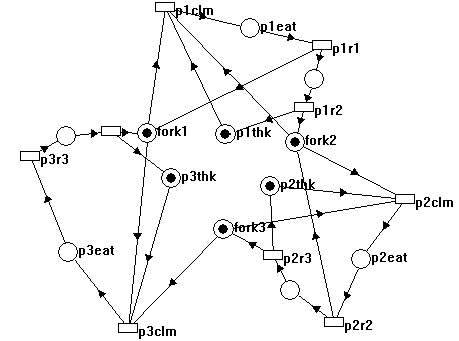
Figure 22. Radical philosophers don't starve!
What happens here is that WaitForMultipleObjects has the unique capability of waiting until all mutexes have signaled and then unsignaling them, all in one atomic operation! If you have ever tried to implement this, you know that it is really tough. One would first have to preclaim all of the objects but devise some way to make sure that the thread is not blocked while doing that. If all objects could be claimed, grab them for good; if not, we might run into a circular wait/deadlock condition, so better give up some preclaimed object to give somebody else the chance to get all of his/her objects. If you are too generous, you might never get all of the objects, or two threads might end up in a rhythm where they always give up the "wrong" objects, so they constantly lock each other out. WaitForMultipleObjects is a great synchronizer that relieves programmers from a lot of hassle.
This triptych of articles—"Detecting Deadlocks in Multithreaded Win32 Applications," "The Implementation of DLDETECT.EXE," and this article—is an experiment for the Development Library in that these articles feature a rather lengthy and theoretical approach to multithreading, a new feature in the Win32 API. Although it may sound discouraging at first to be asked to go through a rather theoretical framework first before tackling multithreading, I suspect that studying this material and putting it to use when designing multithreaded applications is well worth the effort. In particular, Petri nets are able to provide a very solid conceptual understanding of the subtleties of multithreading in the Win32 API; along with net invariants, they enable the application designer to analyze an application-in-progress with regard to possible deadlocking and race conditions and to simulate the applications in a Petri net model.
The Microsoft Developer Network Technology Group would love to get your feedback if you decide to adopt this theoretical framework for your own application development. If you happen to find this to be useful, we may very well put a stronger emphasis on applications of Computer Science theory in future articles.
Asche, Ruediger. "Detecting Deadlocks in Multithreaded Win32 Applications." (MSDN Library, Technical Articles)
Asche, Ruediger. "The Implementation of DLDETECT.EXE." (MSDN Library, Technical Articles)
Murata, Tadao. "Petri Nets: Properties, Analysis and Applications." Proceedings of the IEEE 77 (April 1989): 541-580.
Peterson, James L. Petri Nets and the Modeling of Systems. Englewood Cliffs, N.J: Prentice-Hall, 1981.
Reisig, W. A Primer in Petri Net Design. Berlin: Springer-Verlag, 1992.