Dennis Crain
Microsoft Developer Network Technology Group
Created: December 1, 1993
Click to open or copy the files in the VECTOR2D sample application for this technical article.
This article discusses two-dimensional vectors and their use in graphics, and basic vector operations. Their implementation is provided in C. The article also includes a typical application (finding the point nearest a line) that uses vectors to illustrate the utility of vectors and operations on vectors. A Microsoft® Windows NT™ dynamic-link library (DLL) and source code implement a basic library of two-dimensional vector operations.
From its inception, the Microsoft® Windows™ operating system has provided basic two-dimensional graphics capabilities such as clipping, line drawing, shapes such as polygons, and so on. The Windows NT™ operating system takes this capability a step further by including two-dimensional transformations to rotate, scale, translate, shear, and reflect graphics objects as well as Bézier curves and wide pens. This is great, but there are still a ton of things that a graphics application must do itself to achieve respectability.
For example, how do you determine the distance of a given point from a line or a curve? How do you determine the reflection of a ray from a surface? One thing these questions have in common is that they both can be solved by using vectors and operations on those vectors. This article discusses the basics of two-dimensional vectors and vector operations. A C implementation of these concepts is provided in the body of the article and as sample code implementing the vector operations in a Windows NT dynamic-link library (DLL). View this article and its associated code as a first step to building a significant library of graphics tools that will allow you to write that fully featured, two-dimensional graphics application. Future articles will deal with more advanced graphics topics that use the vector operations discussed in this article.
If you are thinking "Just what is a vector?", this section is for you! It's really not uncommon to wonder what a vector is. If your graphics programming experience has been limited to Windows and your application development did not involve graphics editors of one sort or another, you probably have never dealt with vectors. I will not attempt to describe vectors exhaustively; you can find the details in countless textbooks on the subject. I will describe them to such a point of understanding that we can move on to the practical use of vectors within a two-dimensional graphics application.
An important distinction to make up-front is that a vector is not a point, although the representation is similar for both. For example, a point, p, is typically described using an ordered pair of numbers, for example p = (100, 200). This is commonly interpreted as the point located 100 units in the x direction and 200 units in the y direction from some well-defined and consistent origin. The vector p (denoted as a vector by using bold text), where p = (100, 200), is interpreted very differently. The vector describes displacement. It may originate anywhere in the coordinate system. In this example, the vector is displaced 100 units in the x direction and 200 units in the y direction from some arbitrary point.
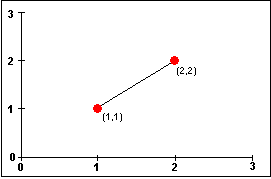
Figures 1 and 2 illustrate these concepts. In Figure 1, a line segment is drawn between the two points. In my attempt to distinguish between points and vectors, the important thing to note is that the points are positions within a coordinate system denoted by the ordered pairs (1, 1) and (2, 2).

Figure 1. Line segment between the points (1, 1) and (2, 2)
Figure 2 shows the vector defined by the same two points—(1, 1) and (2, 2). Because vectors describe displacement, the vector can be represented by the 2-tuple (1, 1). That is, the vector is displaced 1 unit in the x direction and 1 unit in the y direction.
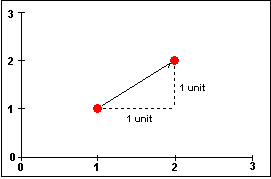
Figure 2. Vector associated with the points (1, 1) and (2, 2)
That brings us to a very useful definition of a vector. The vector p is defined by the difference between the two points used to place the vector in the coordinate space: p = (x2 - x1, y2 - y1). In the example above, the vector p = (2 - 1, 2 - 1), which is simply (1, 1). The vector p in figure 2 is said to be bound to the point (1, 1), although, as Figure 3 illustrates, this vector could easily be bound to any point in the coordinate space. Note that all three vectors are described by the 2-tuple (1, 1).

Figure 3. Vectors may be bound to any point
So much for what a vector is and what it isn't. Let's move on to the various operations that can be performed on vectors.
Vector space? As in "beam me up"? Not quite. As Foley et al. explain it, the vector space is a set composed of vectors upon which addition and scalar multiplication can take place. There are tons of analogies that can give you a sense of what the vector space is. You may want to insert your own at this point. Here are a few of my favorites: Think of the vector space as a croquet court. The vectors are represented by the motion of the balls as you hit them. Vector addition takes place when you place your ball next to your opponent's and smack it 50 feet in the opposite direction. Or there is the pool table analogy. Forget the balls for a moment. Just consider the pool cue. The pool cue has a length, as does a vector. Like a vector, the pool cue is bound to an origin that moves around the table as you try to line up shots. This example helps you think of the vector space in terms of a plane. This should give you a feel for the vector space. So as not to belabor it, let's move on to the motivation for using vectors.
Good question. I have some simple answers. Vectors are convenient. They allow you to do complex things using simple concepts. This simplicity is derived from the fact that, through vectors, many geometric concepts can be expressed algebraically with little consideration of the coordinate system. Vectors simplify your life. Once you have written a vector library, solutions to various graphics problems are reduced to creative use of the functions in your library.
Remember what I said about the vector space? It includes addition and scalar multiplication of vectors. These are the two basic operations from which all vector use is derived. This section discusses vector addition, multiplication, and a few other operations. But remember, each additional operation is simply a use of the two operations found in the vector space—addition and multiplication.
Before jumping off into each operation, let's define the structure used to define a two-dimensional vector in this article and used in the C implementation of each operation. The following structure is composed of two values, the x and y components of the vector. These are doubled to permit the use of real number values. Real numbers are required to fulfill the requirement of scalar multiplication (multiplication by real numbers) in the vector space.
typedef struct tagVECTOR2D {
double x;
double y;
} VECTOR2D, *PVECTOR2D;
Throughout much of this article I will use two vectors, a and b. The a vector is represented by the 2-tuple (4, 5). The b vector is represented by the 2-tuple (2, 3).
Vectors may be added to one another. The vector obtained by the addition of two vectors is nothing more than the sum of the components. This is easily represented as follows: Given two vectors, a and b, the resultant vector c = (a1 + b1, a2 + b2). Using the previously assigned 2-tuples for these vectors, c = (4 + 2, 5 + 3) = (6, 8).
This operation can be implemented in the following code. The parameters v0 and v1 are pointers to VECTOR2D structures that contain the two vectors to be added. The resulting vector is placed in the parameter v, whose address is returned as an indication of the success of the operation.
PVECTOR2D APIENTRY vAddVectors(PVECTOR2D v0, PVECTOR2D v1, PVECTOR2D v)
{
if (v0 == NULL || v1 == NULL)
v = (PVECTOR2D)NULL;
else
{
v->x = v0->x + v1->x;
v->y = v0->y + v1->y;
}
return(v);
}
Figure 4 illustrates the addition of two vectors and the resultant vector. Note that vector addition is not simply a matter of adding the lengths together. That is vector multiplication. Vector addition is a "geometric sort of thing." The sum of the two vectors is a vector that is the sum of the displacements. If you draw a vector from the tail of a to the head of b, as in Figure 4, you can see that the displacement of the vector is the same as that derived algebraically.
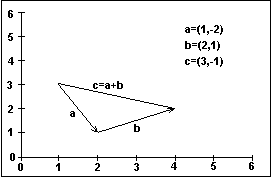
Figure 4. Addition of two vectors
Multiplication of vectors is the second operation required in the vector space. Vectors are most commonly multiplied to produce scaling, or what is known as the dot product. Scaling a vector simply increases the overall displacement of a vector by changing the x and y components of the vector by some scaling factor. The following code demonstrates scaling.
PVECTOR2D APIENTRY vScaleVector(PVECTOR2D v0, double dScaling, PVECTOR2D v)
{
if (v0 == NULL)
v = (PVECTOR2D)NULL;
else
{
if (dScaling != 0)
{
v->x = (v0->x *= dScaling);
v->y = (v0->y *= dScaling);
}
}
return(v);
}
Figure 5 illustrates the scaling of two vectors.
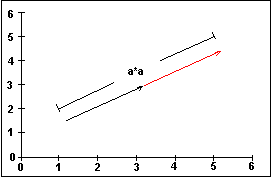
Figure 5. Scaling of two vectors
The dot product of two vectors is the sum of the products of the components of the vectors. The dot product for the vectors a and b is a1 * a2 + b1 * b2. Given the sample vectors (4, 5) and (2, 3), the dot product is 4 * 2 + 5 * 3, or 23. This is easily implemented in the code that follows.
double APIENTRY vDotProduct(PVECTOR2D v0, PVECTOR2D v1)
{
double dotprod;
dotprod = (v0 == NULL || v1 == NULL)
? 0.0
: (v0->x * v1->x) + (v0->y * v1->y);
return(dotprod);
}
Dot products are used frequently in graphics—to determine the angle between vectors, to determine if two vectors are perpendicular, and to decompose a vector into its components. This decomposition (that reminds me of a joke about Beethoven) is what we will use in the next section, which deals with a common problem—selecting a line in a graphics application with a mouse.
This covers the two operations essential to vectors and fulfills the definition of a vector space. Let's now take a look at useful operations derived from the use of vector addition and scalar multiplication.
No rocket science here. Most of us would agree that subtraction is merely addition with a different outlook on life!
PVECTOR2D APIENTRY vSubtractVectors(PVECTOR2D v0, PVECTOR2D v1, PVECTOR2D v)
{
if (v0 == NULL || v1 == NULL)
v = (PVECTOR2D)NULL;
else
{
v->x = v0->x - v1->x;
v->y = v0->y - v1->y;
}
return(v);
}
The length or magnitude of a vector is the distance from the head of the vector to the tail of the vector. Distance is the operative word here. Remember the Pythagorean theorem? It asserts that the distance between two points can be obtained by the following formula:
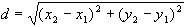
If you have doubts, take a look at a math textbook. Because the components of a two-dimensional vector are the differences between two points, this formula can be restated as follows, given the vector a:
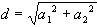
This relationship is easily implemented in the following code.
double APIENTRY vVectorMagnitude(PVECTOR2D v0)
{
double dMagnitude;
if (v0 == NULL)
dMagnitude = 0.0;
else
dMagnitude = sqrt(vVectorSquared(v0));
return (dMagnitude);
}
Let's say you have a really cool application that draws lines on the screen. The product specification states that you must be able to move these lines with a mouse. So, how do you know when you are clicking on the line? The rectangle bounding the line (determined by the endpoints of the line) lets you know that you are "close." That is a great way to indicate that you are even looking for a line, but it is just not good enough for accurately selecting a line. You could try to recall some of that wonderful trigonometry stuff that you learned in high school. You could do something really stupid, like testing the color of the pixel. Or you could use those vectors!
This technique involves resolving the vector between one of the endpoints of the line and the point at which the mouse click occurred into its components. One of the components of this vector is another vector that is perpendicular to the line and passes though the mouse point. The length (or magnitude) of this vector is the distance from the point to the line. Figure 6 illustrates the projection of the "mouse" vector a onto the line and the perpendicular "normal" vector. It is the length of that vector that determines the distance between the point and the line.
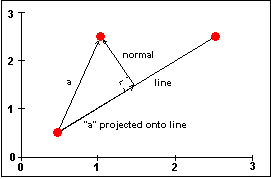
Figure 6. Vectors used to find distance between point and line
Let's take a look at the code.
void APIENTRY vProjectAndResolve(PVECTOR2D v0, PVECTOR2D v1, PPROJECTION ppProj)
{
VECTOR2D ttProjection, ttOrthogonal;
double proj1;
//
//obtain projection vector - v0 onto v1
//
//c = a * b
// ----- b
// |b|^2
//
proj1 = vDotProduct(v0, v1)/vDotProduct(v1, v1);
ttProjection.x = v1->x * proj1;
ttProjection.y = v1->y * proj1;
//
//obtain perpendicular projection : e = a - c
//
vSubtractVectors(v0, &ttProjection, &ttOrthogonal);
//
//fill PROJECTION structure with appropriate values
//
ppProj->LenProjection = vVectorMagnitude(&ttProjection);
ppProj->LenPerpProjection = vVectorMagnitude(&ttOrthogonal);
ppProj->ttProjection.x = ttProjection.x;
ppProj->ttProjection.y = ttProjection.y;
ppProj->ttPerpProjection.x = ttOrthogonal.x;
ppProj->ttPerpProjection.y = ttOrthogonal.y;
}
VECTOR2D.DLL is a dynamic-link library for Windows NT. It includes all of the functions described in this article—and some functions not discussed in the article. The source code is included. You may use the DLL as-is or add functions to it.
The following macro and functions are contained within the DLL.
The POINTS2VECTOR2D macro converts two points to a two-dimensional vector.
Syntax
POINTS2VECTOR2D(pt0, pt1, vect)
Parameters
| pt0 | A POINT structure containing the first coordinate of the two-dimensional vector. |
| pt1 | A POINT structure containing the second coordinate of the two-dimensional vector. |
| vect | A VECTOR2D structure in which the x and y components of the two-dimensional vector are placed. |
Return value
None.
The vAddVectors function adds the components of one two-dimensional vector to another. The resultant vector c = (a1 + b1, a2 + b2).
Syntax
PVECTOR2D vAddVectors(PVECTOR2D v0, PVECTOR2D v1, PVECTOR2D v);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the components of the first two-dimensional vector. |
| v1 | A pointer to a VECTOR2D structure containing the components of the second two-dimensional vector. |
| v | A pointer to a VECTOR2D structure in which the components of the two-dimensional vector obtained from the addition of the first two are placed. |
Return value
A pointer to a VECTOR2D structure containing the new vector obtained from the addition of the first two parameters.
The vDistFromPointToLine function computes the distance from the point ptTest to the line defined by endpoints pt0 and pt1. This is done by resolving the vector from pt0 to ptTest into its components. The length of the component vector that is attached to the head of the vector from pt0 to ptTest is the distance of ptTest from the line.
Syntax
double vDistFromPointToLine(LPPOINT pt0, LPPOINT pt1, LPPOINT ptTest);
Parameters
| pt0 | A pointer to a POINT structure containing the first endpoint of the line. |
| pt1 | A pointer to a POINT structure containing the second endpoint of the line. |
| ptTest | A pointer to a POINT structure containing the point for which the distance from the line is to be computed. |
Return value
A double value that contains the distance of ptTest to the line defined by the endpoints pt0 and pt1.
The vDotProduct function computes the dot product of two vectors. The dot product of two vectors is the sum of the products of the components of the vectors; that is, for the vectors a and b, the dot product = a1 * a2 + b1 * b2.
Syntax
double vDotProduct(PVECTOR2D v0, PVECTOR2D v1);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the first vector used for obtaining a dot product. |
| v1 | A pointer to a VECTOR2D structure containing the second vector used for obtaining a dot product. |
Return value
A double value containing the scalar dot product value.
The vIsPerpendicular function determines if two vectors are perpendicular to one another by testing the dot product of the two vectors. If the dot product is zero, the vectors are perpendicular.
Syntax
BOOL vIsPerpendicular(PVECTOR2D v0, PVECTOR2D v1);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the first vector. |
| v1 | A pointer to a VECTOR2D structure containing the second vector. |
Return value
TRUE if the two vectors are perpendicular; FALSE if the vectors are not perpendicular.
The vLinearCombination function scales the components of two vectors and adds them together to form a new vector having the linear combination. The resultant vector where u and v are scaling factors and a and b are vectors is c = ua + vb.
Syntax
PVECTOR2D vLinearCombination(PVECTOR2D ptScale, PVECTOR2D v0, PVECTOR2D v1,
PVECTOR2D v);
Parameters
| ptScale | A pointer to a VECTOR2D structure containing the scaling values. |
| v0 | A pointer to a VECTOR2D structure containing the first of two vectors to be combined linearly. |
| v1 | A pointer to a VECTOR2D structure containing the second of two vectors to be combined linearly. |
| v | A pointer to a VECTOR2D structure in which the results of linearly combining vectors v0 and v1 are stored. |
Return value
A pointer to a VECTOR2D structure containing a vector that is the result of the linear combination.
A normalized vector is a vector with a length of 1. The resultant vector is often called a unit vector. The vNormalizeVector function converts a vector into a normalized vector. To normalize a vector, the vector is scaled by the reciprocal of the magnitude of the vector: cn = c * 1/|c|.
Syntax
void vNormalizeVector(PVECTOR2D v0);
Parameter
| v0 | A pointer to a VECTOR2D structure containing the vector to normalize. |
Return value
Void.
The vNormalVector function computes the vector that is normal to a given vector. For the vector a, the normal vector n = (-ay, ax).
Syntax
PVECTOR2D vNormalVector(PVECTOR2D v0, PVECTOR2D v);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the vector for which a normal vector is sought. |
| v | A pointer to a VECTOR2D structure containing the computed normal vector. |
Return value
A pointer to a VECTOR2D structure containing the normal vector.
The vScaleVector function scales the components of a vector by a user-supplied scaling factor.
Syntax
PVECTOR2D APIENTRY vScaleVector(PVECTOR2D v0, double dScaling, PVECTOR2D v);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the components of the two-dimensional vector to be scaled. |
| dScaling | The value by which to scale the components of v0. |
| v | A pointer to a VECTOR2D structure in which the results of multiplying (scaling) the components of v0 by dScaling are stored. |
Return value
A pointer to a VECTOR2D structure containing the scaled vector.
The vSubtractVectors function subtracts the components of one two-dimensional vector from another. The resultant vector c = (a1 - b1, a2 - b2).
Syntax
PVECTOR2D vSubtractVectors(PVECTOR2D v0, PVECTOR2D v1, PVECTOR2D v);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the components of the first two-dimensional vector. |
| v1 | A pointer to a VECTOR2D structure containing the components of the second two-dimensional vector. |
| v | A pointer to a VECTOR2D structure in which the components of the two-dimensional vector obtained from the subtraction of the first two are placed. |
Return value
A pointer to a VECTOR2D structure containing the new vector obtained from the subtraction of the first two parameters.
The vPointNormalForm function computes the components of the point normal equation of a line in a plane vector that is normal to a given vector. For the vector a, the normal vector n = (-ay, ax).
Syntax
BOOL vPointNormalForm(PVECTOR2D v0, PVECTOR2D v1, PPOINTNORMAL ppnPointNormal);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the vector for which a normal vector is sought. |
| v1 | A pointer to a VECTOR2D structure containing the computed normal vector. |
| ppnPointNormal | A pointer to a VECTOR2D structure to contain the normal vector. |
Return value
TRUE if the normal vector is computed successfully; FALSE if it is not.
The vProjectAndResolve function resolves a vector into two vector components. The first is a vector obtained by projecting vector v0 onto v1. The second is a vector that is perpendicular (normal) to the projected vector. It extends from the head of the projected vector v1 to the head of the original vector v0.
Syntax
void vProjectAndResolve(PVECTOR2D v0, PVECTOR2D v1, PPROJECTION ppProj);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the vector for which a normal vector is sought. |
| v1 | A pointer to a VECTOR2D structure containing the original line converted to a vector. |
| ppProj | A pointer to a PROJECTION structure containing the resolved vectors and their lengths. |
Return value
Void.
The vVectorAngle function computes the cosine of the angle between two vectors.
Syntax
double vVectorAngle(PVECTOR2D v0, PVECTOR2D v1);
Parameters
| v0 | A pointer to a VECTOR2D structure containing the first vector. |
| v1 | A pointer to a VECTOR2D structure containing the second vector. |
Return value
A double value indicating the cosine of the angle between the two vectors.
The vVectorMagnitude function determines the length of a vector by summing the squares of each component of the vector. The magnitude is equal to a.x * a.x + a.y * a.y.
Syntax
double vVectorMagnitude(PVECTOR2D v0);
Parameter
| v0 | A pointer to a VECTOR2D structure containing the vector upon which to determine the magnitude. |
Return value
A double value that is the magnitude of the vector.
The vVectorSquared function squares each component of the vector and adds them together to produce the squared value of the vector. SquaredValue = a.x * a.x + a.y * a.y.
Syntax
double vVectorSquared(PVECTOR2D v0);
Parameter
| v0 | A pointer to a VECTOR2D structure containing the vector upon which to determine the squared value. |
Return value
A double value that is the squared value of the vector.
Computer Graphics. Hill, F. S., Jr. 1990, Macmillan: New York, NY.
Computer Graphics: Principles and Practices (2nd ed). Foley, J. D.; van Dam, A.; Feiner, S. K.; and Hughes, J. F. 1990, Addison-Wesley: Reading, MA.
Graphics Gems. Glassner, A. S. (ed) 1990, Academic Press: San Diego, CA.