15.16.2 Division Operator /
Gallia est omnis divisa in partes tres.
—Julius Caesar, Commentaries on the Gallic Wars (58 B.C.)
The binary / operator performs division, producing the quotient of its operands.
The left-hand operand is the dividend and the right-hand operand is the divisor.
Integer division rounds toward 0. That is, the quotient produced for operands n and d that are integers after binary numeric promotion (§5.6.2) is an integer value q whose magnitude is as large as possible while satisfying  ; moreover, q is positive when
; moreover, q is positive when 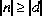 and n and d have the same sign, but q is negative when
and n and d have the same sign, but q is negative when  and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is
and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is -1, then integer overflow occurs and the result is equal to the dividend. Despite the overflow, no exception is thrown in this case. On the other hand, if the value of the divisor in an integer division is 0, then an ArithmeticException is thrown.
The result of a floating-point division is determined by the specification of IEEE arithmetic:
- If either operand is NaN, the result is NaN.
- If the result is not NaN, the sign of the result is positive if both operands have the same sign, negative if the operands have different signs.
- Division of an infinity by an infinity results in NaN.
- Division of an infinity by a finite value results in a signed infinity. The sign is determined by the rule stated above.
- Division of a finite value by an infinity results in a signed zero. The sign is determined by the rule stated above.
- Division of a zero by a zero results in NaN; division of zero by any other finite value results in a signed zero. The sign is determined by the rule stated above.
- Division of a nonzero finite value by a zero results in a signed infinity. The sign is determined by the rule stated above.
- In the remaining cases, where neither an infinity, nor a zero, nor NaN is involved, the quotient is computed. If the magnitude of the quotient is too large to represent, we say the operation overflows; the result is then an infinity of appropriate sign. If the magnitude is too small to represent, we say the operation underflows and the result is then a zero of appropriate sign. Otherwise, the quotient is rounded to the nearest representable value using IEEE 754 round-to-nearest mode. The Java language requires support of gradual underflow as defined by IEEE 754 (§4.2.4).
Despite the fact that overflow, underflow, division by zero, or loss of information may occur, evaluation of a floating-point division operator / never throws a run-time exception.
 ; moreover, q is positive when
; moreover, q is positive when 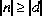 and n and d have the same sign, but q is negative when
and n and d have the same sign, but q is negative when  and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is
and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is