Wraps

You can use a wrap to calculate texture coordinates for a face or mesh. To create a wrap, the application must specify a type, a reference frame, an origin, a direction vector, and an up vector. The application must also specify a pair of scaling factors and an origin for the texture coordinates.

Your application calls the IDirect3DRM3::CreateWrap function to create an IDirect3DRMWrap interface. This interface has two unique methods: IDirect3DRMWrap::Apply, which applies a wrap to the vertices of the object, and IDirect3DRMWrap::ApplyRelative, which transforms the vertices of a wrap as it is applied.

In the examples, the direction vector (the v vector) lies along the z-axis, and the up vector (the u vector) lies along the y-axis, with the origin at [0 0 0].

For a reference to the methods of the IDirect3DRMWrap interface, see IDirect3DRMWrap.

This section describes the wrapping flags and the four wrapping types.

Wrapping Flags
Flat
Cylindrical
Spherical
Chrome

Wrapping Flags

The D3DRMMAPPING type includes the D3DRMMAP_WRAPU and D3DRMMAP_WRAPV flags. These flags determine how the rasterizer interprets texture coordinates. The rasterizer always interpolates the shortest distance between texture coordinates—that is, a line. The path taken by this line, and the valid values for the u- and v-coordinates, varies with the use of the wrapping flags. If either or both flags is set, the line can wrap around the texture edge in the u or v direction, as if the texture had a cylindrical or toroidal topology.

In flat wrapping mode, in which neither of the wrapping flags is set, the plane specified by the u- and v-coordinates is an infinite tiling of the texture. In this case, values greater than 1.0 are valid for u and v. The shortest line between (0.1, 0.1) and (0.9, 0.9) passes through (0.5, 0.5).
If either D3DRMMAP_WRAPU or D3DRMMAP_WRAPV is set, the texture is a cylinder with an infinite length and a circumference of 1.0. Texture coordinates greater than 1.0 are valid only in the dimension that is not wrapped. The shortest distance between texture coordinates varies with the wrapping flag; if D3DRMMAP_WRAPU is set, the shortest line between (0.1, 0.1) and (0.9, 0.9) passes through (0, 0.5).
If both D3DRMMAP_WRAPU and D3DRMMAP_WRAPV are set, the texture is a torus. Because the system is closed, texture coordinates greater that 1.0 are invalid. The shortest line between (0.1, 0.1) and (0.9, 0.9) passes through (0, 0).

Although texture coordinates that are outside the valid range may be truncated to valid values, this behavior is not defined.

Typically, applications set a wrap flag for cylindrical wraps when the intersection of the texture edges does not match the edges of the face; applications do not set a wrap flag when more than half of a texture is applied to a single face.

Flat

The flat wrap conforms to the faces of an object as if the texture were a piece of rubber that was stretched over the object.

The [u v] coordinates are derived from a vector [x y z] by using the following equations:

In these formulas, s is the window-scaling factor and o is the window origin. The application should choose a pair of scaling factors and offsets that map the ranges of x and y to the range from 0 to 1 for u and v.

Cylindrical

The cylindrical wrap treats the texture as if it were a piece of paper that is wrapped around a cylinder so that the left edge is joined to the right edge. The object is then placed in the middle of the cylinder and the texture is deformed inward onto the surface of the object.

For a cylindrical texture map, the effects of the various vectors are shown in the following illustration.

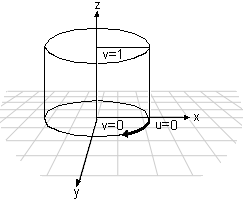
Diagram showing the effects of vectors on a cylindrical wrap

The direction vector specifies the axis of the cylinder, and the up vector specifies the point on the outside of the cylinder where u equals 0. To calculate the texture [u v] coordinates for a vector [x y z], the system uses the following equations:

Typically, u would be left unscaled and v would be scaled and translated so that the range of z maps to the range from 0 to 1 for v.

Spherical

For a spherical wrap, the u-coordinate is derived from the angle that the vector [x y 0] makes with the x-axis (as in the cylindrical map) and the v-coordinate from the angle that the vector [x y z] makes with the z-axis. Note that this mapping causes distortion of the texture at the z-axis.

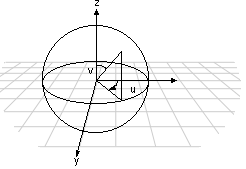
Diagram showing the effects of vectors on a spherical wrap

This translates to the following equations:

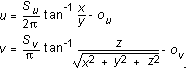
Equations for deriving u-v coordinates from a vector in a spherical wrap

The scaling factors and texture origin will often not be needed here as the unscaled range of u and v is already 0 through 1.

Chrome

A chrome wrap allocates texture coordinates so that the texture appears to be reflected onto the objects. The chrome wrap takes the reference frame position and uses the vertex normals in the mesh to calculate reflected vectors. The texture u- and v-coordinates are then calculated from the intersection of these reflected vectors with an imaginary sphere that surrounds the mesh. This gives the effect of the mesh reflecting whatever is wrapped on the sphere.