Description
This sample program shows how palette changes can create an animated effect.
Path
Source: (SDK root)\Samples\Multimedia\DDraw\Src\Wormhole
Executable: (SDK root)\Samples\Multimedia\DDraw\Bin\Wormhole.exe
User's Guide
Press F12 or ESC to quit the program.
Programming Notes
Imagine a 4x4 display using 4 colors. We could set the colors up to look something like this:

Now we can cycle all of the colors in each row to the right. The one on the right will wrap around to the left.

If we continue this cycling we would get animated lines moving to the right. The same can be done to animate the lines going down:
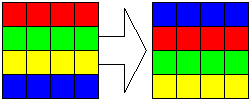
Now if we expand our palette to 16 color we can combine moving down and right at the same time.
Move right:
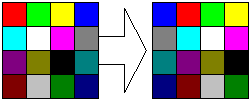
Move down:
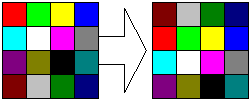
Move right and down:

Now if you tile these 4x4 blocks end to end and cycle the colors as shown, you get a moving checkerboard. Wormhole does the same thing, except that it uses 15x15 blocks (225 colors) and instead of tiling the blocks end to end on a flat plane, it tiles them in 3-D converging at the center of the wormhole.
The following code will generate the 3-D wormhole using the aforementioned 15x15 grids:
//Do all the work!
//convert r,theta,z to x,y,x to screen x,y
//plot the point
//z=-1.0+(log(2.0*j/DIVS) is the line that sets the math eqn for plot
//Feel free to try other functions!
//Cylindrical coordinates, e.g. z=f(r,theta)
#define STRETCH 25
#define PI 3.14159265358979323846
#define XCENTER 160
#define YCENTER 50
#define DIVS 1200
#define SPOKES 2400
void transarray(void)
{
float x,y,z;
int i,j,color;
for(j=1;j<DIVS+1;j++)
for(i=0;i<SPOKES;i++)
{
z=-1.0+(log(2.0*j/DIVS));
x=(320.0*j/DIVS*cos(2*PI*i/SPOKES));
y=(240.0*j/DIVS*sin(2*PI*i/SPOKES));
y=y-STRETCH*z;
x+=XCENTER;
y+=YCENTER;
color=((i/8)%15)+15*((j/6)%15)+1;
if ((x>=0)&&(x<=320)&&(y>=0)&&(y<=200))
plot((int) x,(int) y,color);
}
}
After loading the bitmap to a DirectDraw surface, all that is left to do is rotate the colors and you have a wormhole.