DAStatics Functions Relevant to DAGeometry Objects

ImportGeometry Creates a DAGeometry by synchronously importing the given .x file.

ImportGeometryAsync Asynchronously imports the given .x file.

SoundSource Creates a DAGeometry object that contains sound.

SpotLight Creates a spotlight geometry. Same as SpotLightAnim except that cutoff is a nonanimated number (a double).

SpotLightAnim Creates a spotlight geometry.

TriMesh Creates a set of triangle meshes that you can use to construct almost any geometry.

UnionGeometry Creates a DAGeometry object by combining the given geometries.

UnionGeometryArray Creates a geometry behavior by combining the geometries in the array.

ImportGeometry

DAStatics Class

Creates a DAGeometry by synchronously importing the given .x file. Synchronous loads are blocking calls, which means that ticking will not continue on any model until all synchronous downloads are completed. These downloads should be small and listed before asynchronous downloads. Use asynchronous downloads for more complex images and sounds. See ImportGeometryAsync for a description of the asynchronous import function.

Syntax

lib.ImportGeometry( url )

Parameters

url
Path name (a string) of the file to be downloaded.

Return Value

Returns the DAGeometry object.

ImportGeometryAsync

DAStatics Class

Asynchronously imports the given .x file. Asynchronous downloads should be listed after synchronous ones and used for more complex sounds and images. For a description of the synchronous import function, see ImportGeometry.

Syntax

lib.ImportGeometryAsync( url, geoStandIn )

Parameters

url
Path name (a string) of the geometry to be downloaded.
geoStandIn
Geometry to use while the contents at url are still being downloaded. This argument cannot be null.

Return Value

Returns the DAImportationResult object, which has the following relevant properties:

CompletionEvent, which is the event that triggers once the download is complete.
Geometry, which is the imported DAGeometry object.
Progress, which is the progress of the download.
Size, which is the size of the download.

SoundSource

DAStatics Class

Creates a DAGeometry object that contains sound. The bounding box is the empty bounding box, where the maximum coordinate is less than the minimum coordinate.

Syntax

lib.SoundSource( sound )

Parameters

sound
DASound object that is contained within the geometry.

Return Value

Returns the DAGeometry object.

SpotLight

DAStatics Class

Creates a spotlight geometry. Same as SpotLightAnim except that cutoff is a nonanimated number (a double). Note that fullcone is still an animated number (a DANumber).

Syntax

lib.SpotLight( fullcone, cutoff )

Parameters

fullcone
DANumber object specifying, in radians, the half-angle of the region that will receive the full intensity of the spotlight. This parameter can have values from 0.00 to pi. This must be an animated number.
cutoff
A double value specifying, in radians, the half-angle of the region beyond which surfaces receive no illumination. This parameter can have values from the value of fullcone to pi. This is a nonanimated number.

Return Value

Returns the DAGeometry object.

SpotLightAnim

DAStatics Class

Creates a spotlight geometry. A spotlight is a positioned, directed light source initially located at the origin and directed along the negative z-axis. Examples of real-world spotlights include desk lamps, headlights, and flashlights. The bounding box is the empty bounding box, where the maximum extent is less than the minimum extent.

Syntax

lib.SpotLightAnim( fullcone, cutoff )

Parameters

fullcone
DANumber object specifying, in radians, the half-angle of the region that will receive the full intensity of the spotlight. This parameter can have values from 0.00 to pi. This must be an animated number.
cutoff
DANumber object specifying, in radians, the half-angle of the region beyond which surfaces receive no illumination. This parameter can have values from the value of fullcone to pi. This must be an animated number.

Return Value

Returns the DAGeometry object.

Remarks

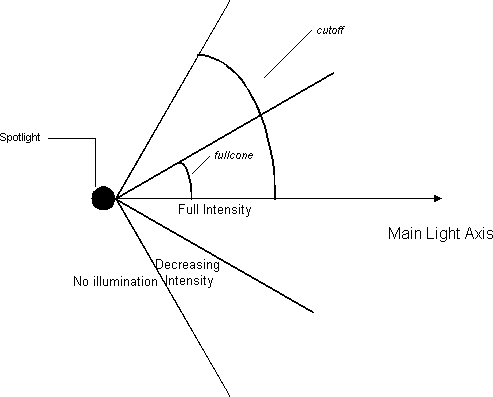
Surfaces receive illumination from the spotlight in the following manner.

If the surface point is within fullcone radians of the main spotlight axis, the spotlight acts as a point light source (including distance attenuation effects).
If the surface point is greater than fullcone radians, but is within cutoff radians of the main spotlight axis, the surface receives illumination that is attenuated by the angular displacement.
If the surface point is greater than cutoff radians from the main spotlight axis, it receives no illumination.

These rules are illustrated in the following diagram.

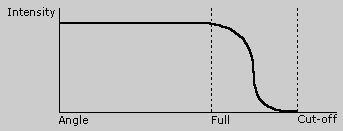
The following diagram shows how the intensity of the spotlight changes in relationship to the angle.

TriMesh

DAStatics Class

Creates a set of triangle meshes that you can use to construct almost any geometry.

Note You can only use this function with Microsoft® DirectAnimation® versions later than 6.0; for example, version 6.00.06.xxx or later. Versions with this function are available in Microsoft Internet Explorer 5, Microsoft Windows® 98 Second Edition, and Windows 2000.

Syntax

lib.TriMesh( nTriangles, positions, normals, surfCoords, indices )

Parameters

nTriangles
Integer specifying the number of triangles in the mesh.
positions
Array (variant) that, for each triangle in the mesh, gives the 3-D locations of the three triangle vertices. The array of vertex positions cannot be empty (have no vertex positions). Positions can either be an array of DAPoint3 objects or a flat array (for example, V1x, V1y, V1z, V2x, V2y, V2z, V3x, V3y, V3z, ...) of floating-point triples. For the floating-point types, the number of values in the array must be a multiple of three.

normals
Array (variant) that, for each triangle vertex in the mesh, contains a vector that is perpendicular to the theoretical underlying surface of the vertex and points toward the outside of the surface. Normals can either be an array of DAVector3 objects or a flat array (for example, V1x, V1y, V1z, V2x, V2y, V2z, V3x, V3y, V3z, ...) of floating-point triples. For the floating-point types, the number of values in the array must be a multiple of three. This array must contain at least one normal. All normals are set to unit length on construction of the mesh, so you don't need to worry about the length of the normals, as long as they are nonzero.

surfCoords
Array (variant) that, for each triangle vertex in the mesh, contains the 2-D location of the vertex on the surface of the underlying theoretical object. For example, on a sphere, the 2-D coordinates could correspond to latitude and longitude. Surface coordinates consist of an up value (u) that lies along the y-axis, and a direction value (v) along the z-axis. Surface coordinates can either be an array of DAPoint2 objects, or a flat array (for example, U1, V1, U2, V2, U3, V3, ...) of floating-point doubles. For the floating-point types, the number of values in the array must be a multiple of two. This array must contain at least one surface coordinate.
indices
Array (variant) that specifies the vertices of each triangle in the mesh. The first six values in indices specify step-stride information, and the rest of the values are indices that point to values in the positions, normals, and surfCoords arrays to describe each vertex in order, and construct triangles three vertices at a time. The first vertex is vertex 0. The indices are a flat array of integer triples. See Remarks for more information and examples. This array can be null, in which case the vertices are accessed sequentially from the other arrays.

Return Value

Returns the DAGeometry object.

Remarks

The front face of each triangle is defined by the counterclockwise orientation of the triangle vertices. As you look at the front of the triangle, the vertices should proceed counterclockwise around the boundary.
The simplest indices array is an empty array (null array or zero length). In this case, the vertices are accessed sequentially from the three vertex data arrays, with a triangle constructed three vertices at a time. The positions, normals, and surfCoords arrays must all have 3T elements, where T is the number of triangles. If you are using flat arrays, the positions and normals arrays must contain 3 × 3T floating-point numbers, while the surfCoords array must contain 2 × 3T floating-point numbers.
For example, the following is a triangle mesh with two triangles and an empty indices array.
nTriangles:   2
positions:    P0, P1, P2, P3, P4, P5      (values in the array are DAPoint3 objects)
normals:      N0, N1, N2, N3, N4, N5      (values in the array are DAVector3 objects)
surfCoords:   S0x,S0y, S1x,S1y, S2x,S2y,  (values in the array are floating-point numbers)
              S3x,S3y, S4x,S4y, S5x,S5y
Indices:      null
The resultant triangles from this mesh are:
Triangle 1:  {P0,N0,S0}, {P1,N1,S1}, {P2,N2,S2}
Triangle 2:  {P3,N3,S3}, {P4,N4,S4}, {P5,N5,S5}
An empty indices array is preferable when all of the vertex data are DirectAnimation elements (such as DAPoint3 or DAVector3) rather than floating-point numbers. This is because DirectAnimation elements are specified by reference, so you don't have overhead in specifying a vertex multiple times.
For example, a cube is constructed from 6×2 triangles, which means 36 vertex references in all. However, there are only eight unique vertices in a cube. With floating-point numbers, you have to respecify the full vertex data for each vertex (because floating-point numbers are specified by value), which means data duplication in the unindexed form.
For triangle meshes that are indexed, the indices array contains six integers specifying step-stride information, before the index data.
The step-stride information is contained in the first six integers, as follows:
            [0]  positions Step
            [1]  positions Stride
            [2]  normals Step
            [3]  normals Stride
            [4]  surfCoords Step
            [5]  surfCoords Stride
The step gives the offset to the first element in the indices array that contains the first index for the positions, normals, or surfCoords array, and the stride gives the incremental offset to the next element in the indices array that contains the index for the positions, normals, or surfCoords array.
For example, if indices[0] is 6, then the sixth element in the indices array, indices[6], is the first index for the positions array.
For example, consider a triangle mesh that defines a cube.
nTriangles: 12
positions[0]:  { 1,  1,  1}
positions[1]:  {-1,  1,  1}
positions[2]:  {-1,  1, -1}
positions[3]:  { 1,  1, -1}
positions[4]:  { 1, -1,  1}
positions[5]:  {-1, -1,  1}
positions[6]:  {-1, -1, -1}
positions[7]:  { 1, -1, -1}

normals[0]:    { 1,  0,  0}
normals[1]:    {-1,  0,  0}
normals[2]:    { 0,  1,  0}
normals[3]:    { 0, -1,  0}
normals[4]:    { 0,  0,  1}
normals[5]:    { 0,  0, -1}

surfCoords[0]: { 1, 0 }
surfCoords[1]: { 0, 1 }
surfCoords[2]: { 0, 0 }
surfCoords[3]: { 1, 1 }

indices[ 0, 1]:    6, 3      // positions step, stride
indices[ 2, 3]:    7, 3      // normals step, stride
indices[ 4, 5]:    8, 3      // surfCoords step, stride

// top face
indices[ 6, 7, 8]: 0, 2, 0   // triangle 1, vertex 1,
                             // index to values in positions/normals/surfCoords arrays
indices[ 9,10,11]: 2, 2, 1   // triangle 1, vertex 2,
                             // index in positions/normals/surfCoords arrays
indices[12,13,14]: 1, 2, 2   // triangle 1, vertex 3,
                             // index in positions/normals/surfCoords arrays

indices[15,16,17]: 0, 2, 0   // triangle 2, vertex 1,
                             // index in positions/normals/surfCoords arrays
indices[18,19,20]: 3, 2, 3   // triangle 2, vertex 2,
                             // index in positions/normals/surfCoords arrays
indices[21,22,23]: 2, 2, 1   // triangle 2, vertex 3,
                             // index in positions/normals/surfCoords arrays

// bottom face
indices[24,25,26]: 6, 3, 0   // triangle 3, vertex 1 
indices[27,28,29]: 4, 3, 1   // triangle 3, vertex 2
indices[30,31,32]: 5, 3, 2   // triangle 3, vertex 3

indices[24,25,26]: 6, 3, 0   // triangle 4, vertex 1 
indices[27,28,29]: 7, 3, 3   // triangle 4, vertex 2
indices[30,31,32]: 4, 3, 1   // triangle 4, vertex 3

// left face
indices[33,34,35]: 6, 1, 0   // triangle 5, vertex 1
indices[36,37,38]: 4, 1, 1   // triangle 5, vertex 2
indices[39,40,41]: 5, 1, 2   // triangle 5, vertex 3

indices[42,43,44]: 6, 1, 0   // triangle 6, vertex 1
indices[45,46,47]: 7, 1, 3   // triangle 5, vertex 2
indices[48,49,50]: 4, 1, 1   // triangle 5, vertex 3

// right face
...
// front face
...
// back face
...
In this case, the step-stride information is set for interleaved vertex data—vertex position, then vertex normal, then vertex surface coordinates—and none of the three vertex arrays share the same indices. However, step-stride pairs can be shared for vertex data, or set to repeat a value. Consider the triangle mesh for a flat panel to form a grid of four squares, two triangles per square:
 
nTriangles:  8

positions[0]:  {  0,  0,  0 }
positions[1]:  { .5,  0,  0 }
positions[2]:  {  1,  0,  0 }
positions[3]:  {  0, .5,  0 }
positions[4]:  { .5, .5,  0 }
positions[5]:  {  1, .5,  0 }
positions[6]:  {  0,  1,  0 }
positions[7]:  { .5,  1,  0 }
positions[8]:  {  1,  1,  0 }

normals[0]:    {  0,  0,  1 }     // one normal for entire mesh

surfCoords[0]: {  0,  0 }
surfCoords[1]: { .5,  0 }
surfCoords[2]: {  1,  0 }
surfCoords[3]: {  0, .5 }
surfCoords[4]: { .5, .5 }
surfCoords[5]: {  1, .5 }
surfCoords[6]: {  0,  1 }
surfCoords[7]: { .5,  1 }
surfCoords[8]: {  1,  1 }

indices[0,1]: 7,1     // positions step, stride
indices[1,2]: 6,0     // normals step, stride
indices[3,4]: 7,1     // surfCoords step, stride

indices[6]:   0       // normal index for all vertices

indices[ 7, 8, 9]:  0,1,3    // triangle 1
indices[10,11,12]:  3,1,4    // triangle 2
indices[13,14,15]:  3,4,6    // triangle 3
indices[16,17,18]:  6,4,7    // triangle 4
indices[19,20,21]:  1,2,4    // triangle 5
indices[22,23,24]:  4,2,5    // triangle 6
indices[25,26,27]:  4,5,7    // triangle 7
indices[28,29,30]:  7,5,8    // triangle 8
In this example, normals[0] is reused over and over for each vertex (stride 0), and both the positions and surfCoords share the same index stream (step 7, stride 1). Without the step-stride model, the index array would require 3 properties per vertex times 3 vertices per triangle times 8 triangles, and would equal 72 entries rather than 31. For reasonable grids of this form (for example, 20 × 20), the cost of the step-stride model approaches one third that of the "list everything" model.
The other reason for the step-stride model is that for auto-generated surface coordinates and normals, the step-stride model eliminates indices altogether for some vertex properties, dramatically reducing the size and complexity of meshes.
Whether the mesh topology is described with an empty or nonempty indices array, the topology itself can't change. This means the indices array can't change. Topology is constant in a triangle mesh. If it weren't, the effort to determine how the triangle mesh changes with time would severely hamper performance. New topologies for a given mesh are best handled with a flexible enough initial topology (for example, if a seam is to open in a ball, the seam vertices should not be shared by both sides), or by accessing a new geometry. However, vertex positions, normals, and surface coordinates themselves can change, so that animate positions could be used to model a waving flag, for example.

Example

Note You must have a version of DirectAnimation later than 6.0 installed to display these samples.
The following examples show an octahedron created with an unindexed triangle mesh (no indices array) and an indexed triangle mesh (non-NULL indices array).
Unindexed Sample

Indexed Sample

UnionGeometry

DAStatics Class

Creates a DAGeometry object by combining the given geometries. The new geometry contains all elements of the original geometries. The bounding box of a set of unioned geometries is simply the union of the bounding boxes of each of the geometries.

Syntax

lib.UnionGeometry( g1, g2 )

Parameters

g1 and g2
DAGeometry objects.

Return Value

Returns the DAGeometry object.

UnionGeometryArray

DAStatics Class

Creates a geometry behavior by combining the geometries in the array. The new geometry contains all elements of the original geometries. The bounding box of a set of unioned geometries is simply the union of the bounding boxes of each of the geometries.

Syntax

lib.UnionGeometryArray( geoArray )

Parameters

geoArray
Array of DAGeometry objects.

Return Value

Returns the DAGeometry object.