Rather than storing your records in a simple list, you may decide to optimize performance of your index (and perhaps retrieval of your data records) by building somewhat more complex data structures. Most languages offer you very simple data structures, such as an array. Arrays allow you to keep simple collections of objects, but each object is fixed in size and the array itself is fixed in size at compile time. If you know you may keep 50-75 records, then an array is a good choice; you just need to allocate room for the larger amount, that is, declare an array of 75 records. How many records should you allocate for a phone list? Some of your customers might want to keep a dozen numbers. Others might keep a hundred. A politician might keep a thousand. A large organization might keep ten thousand.
It would be very wasteful to allocate room for 10 000 records, if you only need to keep a few dozen. Each record might be 1K of data, so 10 000 records would take up ten megabytes, quite a lot for your customers who have only a few phone numbers to track. What you need is a collection that grows as you use it.
The Standard Template Library (STL) offers a variety of collection classes to C++ programmers. These come in two flavors: sequence and associative. Sequence collections are used to hold (you guessed it!) sequences of objects, while associative collections help you match up objects with "keys".
The first of the STL sequence collections is a vector. A vector is like an array that grows as you use it. The second sequence collection is the deque. Deque is short for "double-ended queue". In America we talk about lining up for the bus or for a movie, but in Britain they talk about "queuing up". A queue is like a line at the ticket window. The first person on line is served first, all the others queue behind and wait their turn. You can build a data structure that behaves like a queue; objects added to the queue are removed in the order they arrive. This can be very handy when you have a limited resource (such as a printer) to which you must regulate access. Jobs are added to the queue and taken off the queue as the resource becomes available. They are removed on a first in, first out (FIFO) order.
The third and last of the sequence STL collections is the list. A list implements a doubly-linked list collection. To understand this, you must start by understanding a linked list, and to understand this, we should think first about arrays. An array is like an egg carton — there is a space for each object (egg) you want to store, but each carton holds a predetermined number of eggs. If you have a carton for six eggs, you allocate space in your refrigerator for six eggs, whether you have one or six. If you have seven eggs, then you're in trouble, you need another carton or you have to hold the extra egg in your hand all day.
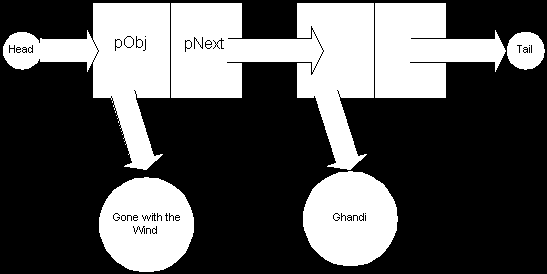
Imagine instead a new kind of egg container. It has space for one egg, but it also has a hook on one side and an eye on the other. If you want to store four eggs, you snap four of these containers together. This results in a little train of cartons, each holding one egg. A linked list is just like such a train. We build a structure called a "node", which holds our object and also points to the next node in the list. The diagram below shows a linked list that we might want to use to store the names of our video tapes:

marks the beginning of the list and it points to the first node. That node keeps a pointer, Head
, to the first video tape and a second pointer, pObj
, which points to the next node in the list. That second node in turn points to a video tape and the next node in the list. It turns out that this is the last node in the list, so it points to tail.pNext
The above example illustrates is a singly-linked list. In a doubly-linked list, nodes not only point to the next node in the list, but also point back to the previous node in the list. This is shown in the diagram below:
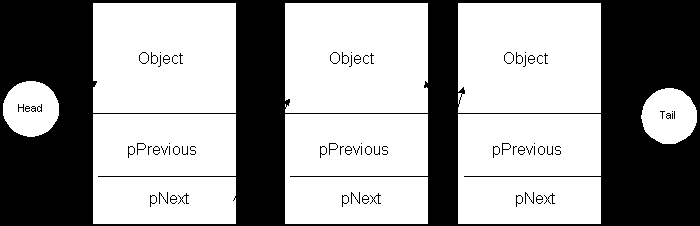
Linked lists are the foundation of a number of other, more complex, data structures. These include B+ trees, Red/Black trees and other intriguing denizens of books and classes on data structures (for example, Algorithms in C++, by Robert Sedgewick, Addison-Wesley ISBN 0-201-51059-6). The essence of each of these structures, however, is to provide enhanced performance. Some data structures are optimized for the ability to add records to the list quickly. Others are optimized for fast searching and/or fast retrieval.
While learning about advanced data structures can be fascinating, the truth is that most often you'll just buy a ready made solution. The most common solution for these problems is a commercial relational database management system or RDBMS.