Aggregation of States

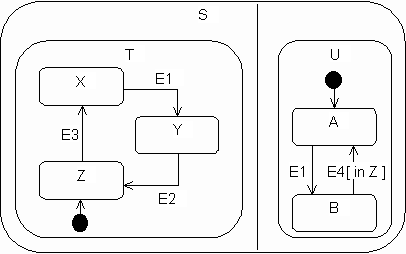
State aggregation is the composition of one state from several other independent states. The composition is of a conjunctive type (composition of type 'and'), which implies that the object must simultaneously be in all the states that constitute the aggregation. State aggregation corresponds to a kind of parallelism between state machines.

The following example illustrates different views of the concept of state aggregation. State

is an aggregation composed of two independent states T
and U
; T
is composed of substates X
, Y
and Z
, and U
is composed of substates A
and B
. The domain of S
is the Cartesian product of T
and U
.

An input transition into state

implies the simultaneous activation of state machines T
and U
, i.e. the object is initially placed in the composite state (Z,A)
. When event E3
occurs, the T
and U
state machines can keep evolving independently, which brings the object to the composite state (X,A)
. State machines T
and U
may also evolve simultaneously, which is the case when event E1
moves the object from composite state (X,A)
to (Y,B)
. Adding conditions to the transitions, such as the guard [in Z]
placed on the transition from B
to A
, makes it possible to introduce dependency relationships between the components of the aggregate. When event E4
occurs, the transition from B
to A
is only valid if the object is also in state Z
at that time.

State aggregation, together with state generalization, simplifies the representation of state machines. Generalization simplifies by factorization, and aggregation simplifies by segmentation of the state space. Without state aggregation, the state machine equivalent to the above would look like this:

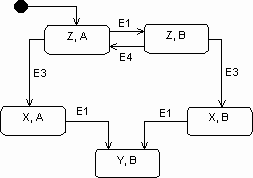
At worst, the number of states of such a 'flat' state machine is equal to the product of the number of states of each component state machine. In the case of an aggregation of three state machines with a few hundred states each (which is already a lot), the equivalent flat state machine could contain up to a million states!