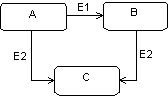
Statechart diagrams may become rather difficult to read when, because of the combinatorial explosion, the number of connections between states becomes high and the resulting diagram can look like a plate of spaghetti!
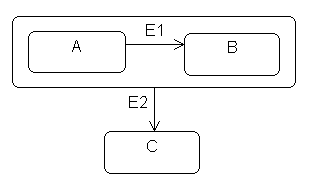
The solution for this situation is to apply the principle of state generalization — the more general states are called superstates, and the more specific states are called substates. The approach to this abstraction proceeds along the same lines as class generalization or specialization. It facilitates representation and makes it possible to mask details.
A state may be decomposed into several disjoint substates, where the substates inherit characteristics from their superstate — in particular, state variables and external transitions. The decomposition into substates is also called disjunctive decomposition (decomposition of type 'exclusive-or'), since an object must be in one and only one substate at a given time.
The following two diagrams illustrate the simplification resulting from state generalization:

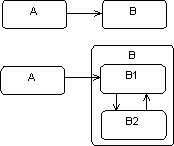
Internal transitions may be inherited, except in the case where the goal of the decomposition into substates is to define a particular state for the treatment of an internal transition. Entry transitions are not inherited by all the states — only one state (the superstate or one of its substates) may be the target of the transition. In the following example, state
is divided into two substates, B
and B1
. The entry transition into state B2
must be deferred onto one of the substates, either directly (as in the case of the following diagram) or indirectly, using an initial nested state.B
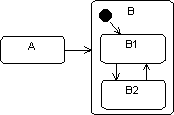
In the above example, state
is connected to substate A
. This situation compromises abstraction and is comparable to a mechanism written according to the specification of a superclass, but with a need to know the details of its subclasses. It is preferable to limit the links between the hierarchical levels of a state machine, by systematically defining an initial (pseudo)state for each level. The diagram below limits the knowledge between levels:B1
Displaying substates exhaustively puts a large information load on the diagrams. The detail of substates may be hidden to give a higher-level perspective. By using stubs, it is possible to show that the input transitions into a composite state refer to a particular substate, without getting into the details of the representation of this substate.
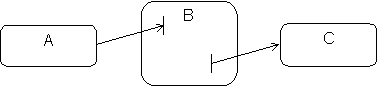
Stubs reduce the information load while showing the presence of substates of B