This next routine, getEntropy, is the main routine for determining which classification is the most important for sales growth. We will turn to communication research and rip off one of their discoveries. As mentioned, entropy is a precise measurement of information.
In a nutshell, entropy is a measure of uncertainty in an observation. The entropy explains the amount of uncertainty about a particular outcome.
This is used a lot in determining information that comes over noisy data lines. We, however, have hijacked it for our marketing purposes.
We will be using logarithms, which happen to be a built-in function in VB 6.0. If you are a bit rusty on them, it simply means that logx = y where (2 to the power y) = x, in this case log has base 2. In English, this means that the log to base 2 of any number is any bits that it would take to represent that many numbers. For example, log2(16) = 4. This tells us that it takes 4 bits to uniquely represent 16 different values. So we will explain this in the code below. But hey, don't worry. We will just use the VB built-in log function to do the dirty work for us.
1. Please add another function to the frmID3 form. Name the function getEntropy and enter the code as shown. This routine will determine the entropy for the classification and return the entropy to the calling routine, determineEntropy.
Public Function getEntropy(ByVal sField As String, itotalRecords As Integer) As Single
'--------------------------------------------------------------
'-- First, determine how many unique values of this field are
'-- in the table. Store them and determine the entropy for each
'--------------------------------------------------------------
Dim sSql As String
Dim adoHoldGroup As ADODB.Recordset
Dim totalUp As Integer
Dim totalDown As Integer
Dim totalSamples As Integer
Dim fractionalEntropy As Single
Dim entropy As Single
Dim searchValue As String
fractionalEntropy = 0
Set adoHoldGroup = New ADODB.Recordset
adoHoldGroup.CursorLocation = adUseClient
'-- grab the info here--
sSql = "SELECT * FROM ID3 ORDER BY " & sField
adoHoldGroup.Open sSql, adoConnection
If (adoHoldGroup.BOF) And (adoHoldGroup.EOF) Then
MsgBox "No records in the ID3 Table"
Exit Function
End If
totalSamples = adoHoldGroup.RecordCount
adoHoldGroup.MoveFirst
searchValue = adoHoldGroup.Fields.Item(sField)
With adoHoldGroup
While Not .EOF
totalUp = 0
totalDown = 0
'---------------------------------------------------
'-- Loop through all of the records with like values
'---------------------------------------------------
Do While (searchValue = .Fields.Item(sField))
If !SalesUp = True Then
totalUp = totalUp + 1
Else
totalDown = totalDown + 1
End If
.MoveNext
If (.EOF) Then Exit Do
Loop
'---------------------------------------------------
'-- Now determine the entropy for that group --
'---------------------------------------------------
If (totalUp = 0) Then
fractionalEntropy = -1#
ElseIf (totalDown = 0) Then
fractionalEntropy = -1#
Else
fractionalEntropy = _
-(totalUp / totalSamples) * Log(totalUp / totalSamples) - _
(totalDown / totalSamples) * Log(totalDown / totalSamples)
End If
fractionalEntropy = (fractionalEntropy / itotalRecords)
entropy = entropy + fractionalEntropy
If (.EOF) Then
getEntropy = entropy + fractionalEntropy
Else
searchValue = adoHoldGroup.Fields.Item(sField)
End If
Wend
End With
End Function
We want all of the records sorted by the particular field we will be examining. So if we are determining the entropy on the CountryLanguage classification, for example, all of the records that have English in the CountryLanguage field will be lumped together.
So what we want to do is loop through the recordset and determine the entropy on each of the records that have the same value in the CountryLanguage field. When the value of the field changes to, say, German, we will stop and calculate the value for English because we know we have looked at each of those. So by returning the records sorted by the classification field, we can be sure that all like records are together. An easy way to do this is to take the first value passed into our getEntropy function, sField. We can dynamically build our SQL statement instructing the recordset to be returned ordered by that field. So if we were determining the CountryLanguage, all entries for English would be together, etc.
'-- grab the info here--
sSql = "SELECT * FROM ID3 ORDER BY " & sField
adoHoldGroup.Open sSql, adoConnection
We start by opening the recordset adoHoldGroup, which gives us all of the records in the ID3 table. Now that the recordset is opened, we to know which classification we will be working with. After all, it might be CountryRegion, CountryLanguage or Country. Well, we passed in the value as a parameter to the function, sField. Let's say that sField contains Country. So we use that variable and pass it to the recordset's Fields.Item() as a parameter. This will return the current value of that field (Country) in the current record. That value, say Spain, is assigned to the variable searchValue. Please notice that this is another example of a generalized routine. We don't hard code in a value, but permit a parameter passed into the routine, sField, to determine what we will be searching on. This allows us to use the same routine to examine each of the three classifications.
adoHoldGroup.MoveFirst
searchValue = adoHoldGroup.Fields.Item(sField)
As mentioned, we want to handle each category. Let's assume that we passed in CountryLanguage as the classification to be evaluated. If the CountryLanguage of the current record is English, then English is assigned to searchValue. As long as the value of the current record's sField (CountryLanguage) is equal to English, we loop through the recordset and increment the totalUp and totalDown fields. We are simply incrementing the totalUp or totalDown fields if that particular record shows that sales were either up or down. So if we had 4 records from four countries that speak English, and three of the countries experienced sales growth while the fourth did not, totalUp would be 3 and totalDown would be 1. As long as the searchValue (say English) is equal to the field being examined (CountryLanguage), the Do loop looks at each record and increments the totalUp or totalDown. In addition, since all of the records with like languages are grouped together, we know we will get them all. Now say the MoveNext goes to the next record and the Fields.Item(CountryLanguage) is now German. The code exits the Do loop and continues.
While Not .EOF
totalUp = 0
totalDown = 0
'---------------------------------------------------
'-- Loop through all of the records with like values
'---------------------------------------------------
Do While (searchValue = .Fields.Item(sField))
If !SalesUp = True Then
totalUp = totalUp + 1
Else
totalDown = totalDown + 1
End If
.MoveNext
If (.EOF) Then Exit Do
Loop
Essentially, we want to see how many records for countries that speak English had sales that were up and how many were down. So we are going to calculate something called fractionalEntropy.
What we want to look at here is the fractionalEntropy when both the totalUp and totalDown are not 0. If one of these were indeed 0, we would get a divide by zero error. So right away this tells us that we want to have enough samples so that typically both the totalUp and totalDown will have a number greater than zero. We calculate the fractionalEntropy because this is currently being calculated for a single, say language. However, we still need to calculate the number for Spanish, French, German, etc. So we call this fractionalEntropy because it is a piece of the total.
If (totalUp = 0) Then
fractionalEntropy = -1#
ElseIf (totalDown = 0) Then
fractionalEntropy = -1#
Else
fractionalEntropy = _
-(totalUp / totalSamples) * Log(totalUp / totalSamples) - _
(totalDown / totalSamples) * Log(totalDown / totalSamples)
End IfWhat we want to do is look at the frequency of an "up" value out of the total values. Let's say that there were 10 countries with the language of English. If 5 were up, then the probability of the language classification having a positive sales growth is 5 out of 10, or 5/10. Likewise, the probability of the language classification having a negative sales growth is also 5/10. In general terms, we can look at the formula like so:
Outcome = - Probability(up) log Probability(up) - Probability(down)
log Probability(down)
In our example we would then have
Outcome = -5/10 log (5/10) - 5/10 log (5/10)
Outcome = 1 (i.e. no change. We can't discern anything here)
The outcome represents the uncertainty of sales going up, based on the information we placed in the ID3 table. This is NOT meant to be a math book, but only to add an element of interest in data mining and show a simple technique on how we can add another dimension to our knowledge of data mining.
fractionalEntropy = (fractionalEntropy / itotalRecords)
entropy = entropy + fractionalEntropy
If (.EOF) Then
getEntropy = entropy + fractionalEntropy
Else
searchValue = adoHoldGroup.Fields.Item(sField)
End If
We then divide the fractionalEntropy by the number of records in the recordset and assign this to fractionalEntropy. Now that we have calculated the fractionalEntropy for say, the English language, we add that to the variable entropy which represents the entire classification. So we would loop through to the next record in the ID3 table and determine the fractionalEntropy for all countries that speak Spanish. When finished, this fractionalEntropy factor for Spanish would be added to the entropy variable. So entropy is cumulative. Each of the fractionalEntropy factors for each language is just added to the variable entropy, which is the sum of each of the similar records.
If we have reached the end of the recordset, we assign the result to the name of the function, getEntropy, and return that value for the recordset based on the criteria we just analyzed. Otherwise, we update the value of searchValue with the current record. The code then jumps to the top of the loop, initializes the variables, and looks at the next group. Notice how we update the fractionalEntropy with the results from each grouping of say, CountryLanguage.
The final value is then returned to the calling routine, determineEntropy, and placed in the array for sorting and display. Let's now take a look at how to sort our array to ensure the lowest entropy value is stored in the first position.
1. Please add a final sub to our frmID3 form called qsort. We will call this to sort the array, Position, so the least entropy factor is in the lowest position. Essentially, this will sort our array in ascending order.
Public Sub qsort(ByRef myArray() As Variant, ByVal iLowBound As Integer, ByVal iHighBound As Integer)
Dim intX As Integer
Dim intY As Integer
Dim intMiddle As Integer
Dim sHoldString As String
Dim varMidBound As Variant
Dim varTmp As Variant
If iHighBound > iLowBound Then
intMiddle = ((iLowBound + iHighBound) \ 2)
varMidBound = myArray(intMiddle, 0)
intX = iLowBound
intY = iHighBound
Do While intX <= intY
'-- if a value lower in the array is > than one --
'-- higher in the array, swap them now --
If myArray(intX, 0) >= varMidBound _
And myArray(intY, 0) <= varMidBound Then
varTmp = myArray(intX, 0)
sHoldString = myArray(intX, 1)
myArray(intX, 0) = myArray(intY, 0)
myArray(intX, 1) = myArray(intY, 1)
myArray(intY, 0) = varTmp
myArray(intY, 1) = sHoldString
intX = intX + 1
intY = intY - 1
Else
If myArray(intX, 0) < varMidBound Then
intX = intX + 1
End If
If myArray(intY, 0) > varMidBound Then
intY = intY - 1
End If
End If
Loop
Call qsort(myArray(), iLowBound, intY)
Call qsort(myArray(), intX, iHighBound)
End If
End Sub
We call this sub from the determineEntropy routine. Notice that we are passing in the array ByRef, or by reference. This is so that qsort actually has the memory location of the array. Passing in the array by reference permits the qsort routine to work on the actual array – not a copy of the array in memory. Passing in by reference is the default behavior of VB. It can make the changes for us here. A quick call to qsort from determineEntropy will sort the array. We can then print the array from determineEntropy and it will now be sorted for us.
The qsort routine works on the divide-and-conquer principle. It splits the array into two groups and then sorts both the top and the bottom. It does this by calling itself to sort each group. When a routine calls itself, that process is called recursion.
If iHighBound > iLowBound Then
intMiddle = ((iLowBound + iHighBound) \ 2)
varMidBound = myArray(intMiddle, 0)
intX = iLowBound
intY = iHighBound
If the upper bound of the array is greater than the lower bound, we want to grab the middle. When we call qsort from determineEntropy, iHighBound = 2 and iLowBound = 0. In the next line we determine the middle of the array – which will be 1. Recall that the entropy value is in position 0 of the array and the classification is in position 1. So varMidBound is assigned the value from myArray(1, 0) which is the entropy value of the classification.
Now we loop as long as the lower bound <= the upper bound variables. If the entropy value stored in element intX (which will be 0 the first time though) is >= the entropy value stored in the middle value And the entropy value stored in the intY element (which will be 2) is <= the middle entropy value, we have some switching to do.
Do While intX <= intY
'-- if a value lower in the array is > than one --
'-- higher in the array, swap them now --
If myArray(intX, 0) >= varMidBound _
And myArray(intY, 0) <= varMidBound Then
So now we just swap what's in position intX with what is in position intY. Then we move the lower and upper boundaries towards each other and do the same test.
varTmp = myArray(intX, 0)
sHoldString = myArray(intX, 1)
yArray(intX, 0) = myArray(intY, 0)
myArray(intX, 1) = myArray(intY, 1)
myArray(intY, 0) = varTmp
myArray(intY, 1) = sHoldString
intX = intX + 1
intY = intY - 1
When intX > intY, the code moves down and calls itself – recursion. The routine is called on the lower part of the array to sort it, then the upper part. This is the divide-and-conquer principle.
Call qsort(myArray(), iLowBound, intY)
Call qsort(myArray(), intX, iHighBound)
Now don't worry if this part looks a bit cryptic. Years are spent in some computer science courses discussing the various sorts and the math behind them. Luckily we can learn from the masters. It's unfortunate that VB does not have any built-in sorting capabilities like qsort. They are built into other languages, such as C.
To sort strings, instead of numbers, some programmers add a hidden list box to the form. The Sorted property is set to True. They just use the AddItem method to add strings in any order. When all of the strings are added, they start at position 0 of the list box and retrieve each of the items. They will of course now be in sorted order. The list box is not visible so the user never sees it, but this is a quick and dirty way to get some quick string sorting done. Unfortunately this will not work for numbers. A 2 would come before a –3, for example. Not exactly precise for our needs!
OK, finished! Press F5 to run your program. Don't forget to add a reference to the Microsoft ActiveX Data Objects 2.0 Library if you haven't done so already. Try the analyzing the various products and see how the results stack up. You are now ready to turn this beauty over to the product manager.

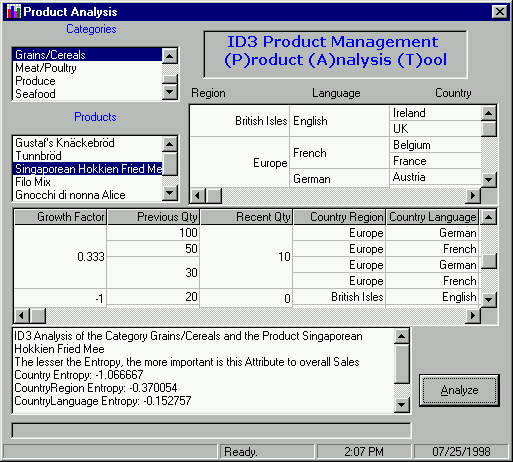
One word on the results. Since we only have a single country for each entry, this usually has the lowest entropy. So we can assume that the country is important. What really makes sense to look at is what is in the second position – after country. In this example for Hokkien Fried Mee, our program says that this is really on the decline in not a single country – but Europe in general! Now this is great information. The product manager might be wondering why sales are down in Germany, without realizing that sales across Europe for this product are in a nose-dive!
I think you can see the value of data mining and hopefully there is enough information provided for you to apply this technique to your real world problems. We re-aggregated the data into a single table. We then tried to find some logical classifications and applied the entropy approach to determine which one of them provided the least uncertainty about sales growth. We tried to illustrate a non-traditional use of database information.