Traversing a Tree: Walking the Code

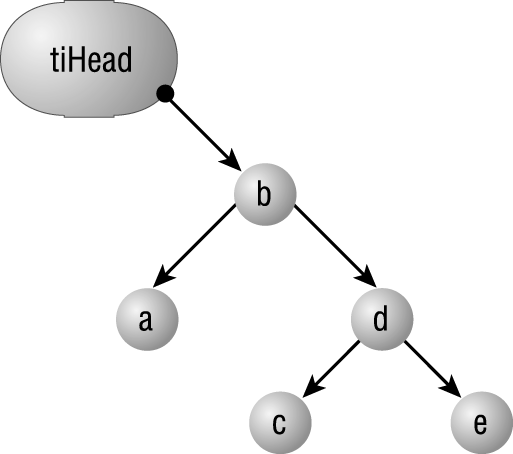
In order to understand tree traversal, assume you’d like to perform a postorder traversal of the tree shown in Figure 6.36. Although this example doesn’t include many nodes, the steps are the same, no matter the size of the tree.

Figure 6.36: Use this small example for the tree traversal example.

To visit each node in the tree using the postorder traversal, follow the steps listed in Table 6.3. (You’ll want to keep a firm finger on the diagram as you work your way through these steps.)

Table 6.3: Recursive Steps to Perform a Postorder Traversal

Level	Action
0	Call the WalkPostOrder method of the Tree class
1	The code in WalkPostOrder calls the PostOrder procedure, passing tiHead as a parameter [Call to Level 2]
2	PostOrder checks to see whether ti (its parameter) is Nothing. It’s not (it’s a reference to the node that contains “b”), so it can continue
2	PostOrder calls itself, passing the left child pointer of the node ti points to (that is, it passes a pointer to the node containing “a”) [Call to Level 3]
3	PostOrder checks to see whether ti (its parameter) is Nothing. It’s not (it’s a reference to the node that contains “a”), so it can continue
3	PostOrder calls itself, passing the left child pointer of the node ti points to (That is, it passes a pointer that is Nothing.) [Call to Level 4]
4	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 3]
3	PostOrder calls itself, passing the right child pointer of the node ti points to (That is, it passes a pointer that is Nothing.) [Call to Level 4]
4	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 3]
3	PostOrder prints its value (“a”) and then returns [Return to Level 2]
2	PostOrder calls itself, passing the right child pointer of the node ti points to (That is, it passes a pointer to the node containing “d”.) [Call to Level 3]
3	PostOrder checks to see whether ti (its parameter) is Nothing. It’s not (it’s a reference to the node that contains “d”), so it can continue
3	PostOrder calls itself, passing the left child pointer of the node ti points to (That is, it passes a pointer to the node containing “c”.) [Call to Level 4]
4	PostOrder checks to see whether ti (its parameter) is Nothing. It’s not (it’s a reference to the node that contains “c”), so it can continue
4	PostOrder calls itself, passing the left child pointer of the node ti points to (That is, it passes a pointer that’s Nothing.) [Call to Level 5]
5	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 4]
4	PostOrder calls itself, passing the right child pointer of the node ti points to (That is, it passes a pointer that’s Nothing.) [Call to Level 5]
5	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 4]
4	PostOrder prints its value (“c”) and then returns [Return to Level 3]
3	PostOrder calls itself, passing the right child pointer of the node ti points to (That is, it passes a pointer to the node containing “e”.) [Call to Level 4]
4	PostOrder checks to see whether ti (its parameter) is Nothing. It’s not (it’s a reference to the node that contains “e”), so it can continue
4	PostOrder calls itself, passing the left child pointer of the node ti points to (That is, it passes a pointer that’s Nothing.) [Call to Level 5]
5	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 4]
4	PostOrder calls itself, passing the right child pointer of the node ti points to (That is, it passes a pointer that’s Nothing.) [Call to Level 5]
5	PostOrder checks to see whether ti (its parameter) is Nothing. It is, so it can’t do anything and just returns [Return to Level 4]
4	PostOrder prints its value (“e”) and then returns [Return to Level 3]
3	PostOrder prints its value (“d”) and then returns [Return to Level 2]
2	PostOrder prints its value (“b”) and then returns to WalkPostOrder [Return toLevel 1, and exit]

Optimizing the Traversals

If you worked your way through the many steps it took to traverse the simple tree, you can imagine how much work it takes to perform the operation on a large tree. You could optimize the code a bit by checking to see whether the child node is Nothing before you recursively call the procedure. That is, you could modify InOrder like this:

Private Sub InOrder(ti As TreeItem)
    If Not ti Is Nothing Then
        If Not ti.LeftChild Is Nothing Then
            Call InOrder(ti.LeftChild)
        End If
        Debug.Print ti.Value; " ";
        If Not ti.RightChild Is Nothing Then
            Call InOrder(ti.RightChild)
        End If
    End If
End Sub

This code would execute a tiny bit faster than the original InOrder tree-traversal procedure (one less procedure call for both children of all the bottom-level nodes), but it’s a little harder to read.

The Sample Project

The code in the sample module performs some simple tree manipulations: it adds nodes, walks the tree in all the traversal orders, and deletes some nodes using the TreeDelete method (not covered in this book, but the code is there in the Tree class for you to use). The first few tests correspond to the tree shown in Figure 6.32 earlier in this chapter, and you can use the code in the project to test your understanding of the different traversal orders.

What Didn’t We Cover?

We actually omitted more about binary trees than we covered here. Binary trees usually fill multiple chapters in textbooks for courses in standard data structures. Consider the following:

Deleting nodes from binary trees is a science unto itself. The sample project includes code to delete nodes from a tree, but it’s just one of many solutions, and possibly not the most efficient one.
Balancing trees is crucial if you want optimized performance. For example, if you add previously sorted data to a tree, you end up with a degenerate tree–all the nodes are linked as the right child of the parent. In other words, you end up with a linked list. Searching through linked lists isn’t particularly efficient, and you lose the benefit of using a binary tree. Courses in data structures normally cover various methods you can use to keep your trees balanced (that is, with the left and right subtrees having approximately the same depth).
In a course on data structures, you’ll normally find a number of variants on binary trees (B-trees, for example) that also take into account data stored on disk.

If you’re interested in finding out more about these variants on binary trees, find a good textbook that focuses on data structures. Of course, most such textbooks are written for Pascal programmers (most universities use Pascal as a teaching language), so you’ll need to do some conversion. It’s not hard, however, once you’ve got the hang of it.