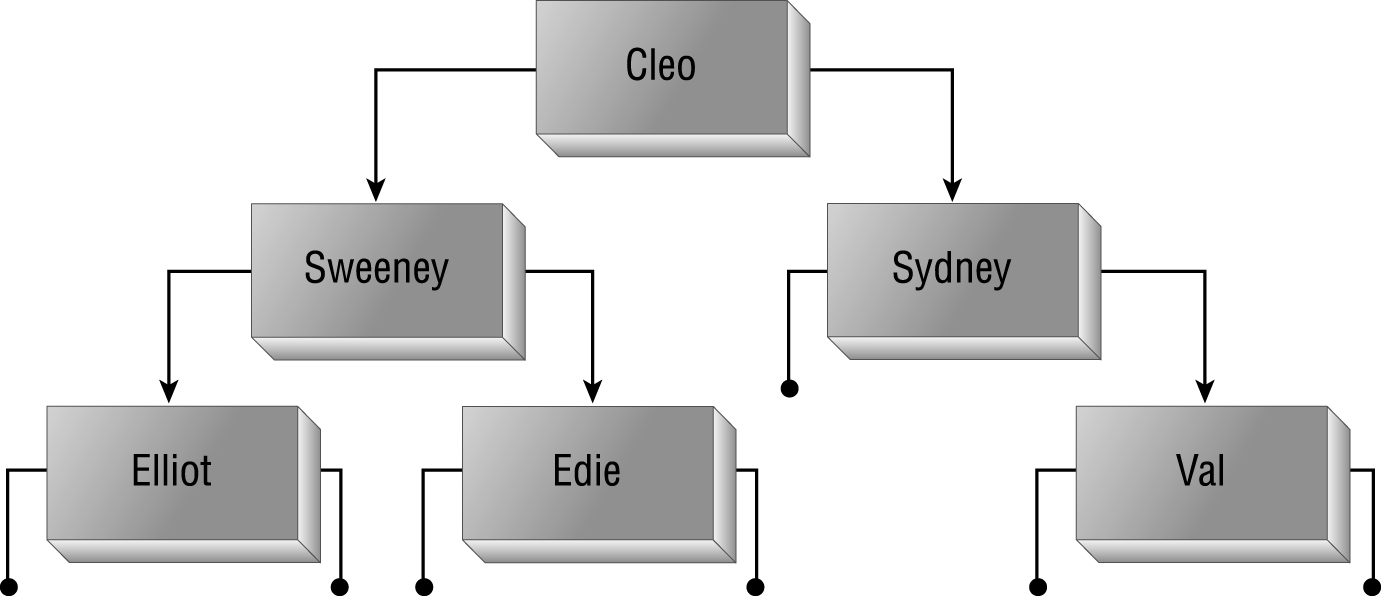
Binary trees have many analogs in the real world. For example, a binary tree can represent a pedigree tree for a purebred cat. Each node represents a cat, with the left and right links to the cat’s two parents. If a parent is unknown, the link will point to Nothing. The diagram in Figure 6.33 shows a parentage tree for a hypothetical purebred cat.

Figure 6.33: A binary tree can represent parentage (two parents per node).
A binary tree can also represent an algebraic expression. If you place algebraic identifiers (constants and variables) in terminal nodes and operators in the interior nodes, you can represent any algebraic expression in a tree. This makes it possible to write expression evaluators: by parsing the expression, placing the various expressions correctly in the tree, and then traversing the tree in the correct order, you can write a simple expression evaluator. The diagram in Figure 6.34 shows how you might represent a simple algebraic expression in a binary tree.
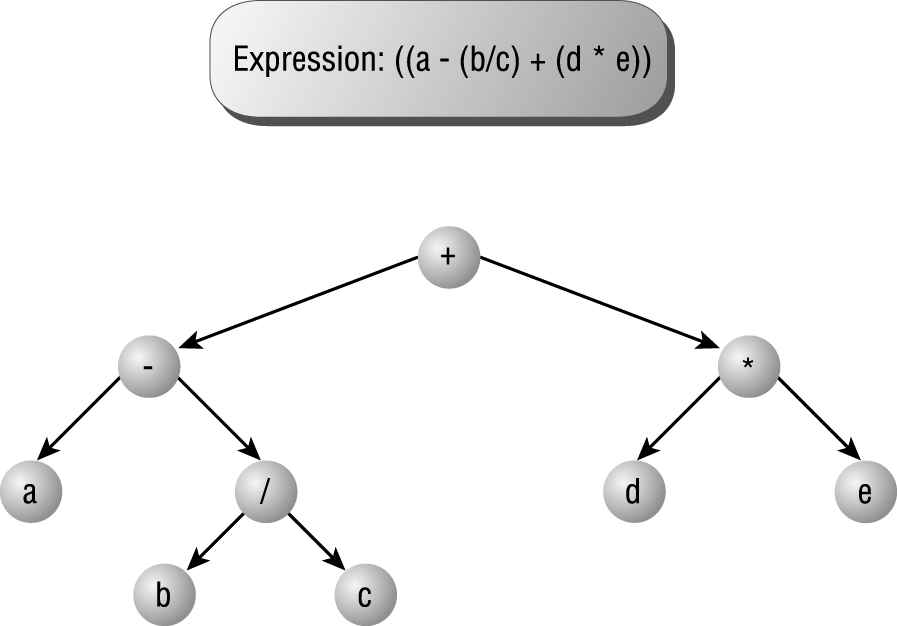
Figure 6.34: A binary tree can represent an algebraic expression.
Depending on how you traverse the tree, you could visit the nodes in any of the following manners.
(a – (b/c) + (d * e))Add(Subtract(a, Divide(b, c)), Multiply(d, e))Push a, Push b, Push c, Divide, Subtract, Push d, Push e, Multiply, Add