Implementing the drunkard’s walk search algorithm (CoordCheckMap) is a relatively simple task. As in the ColorCheckMap function, this search is called with three arguments: the window handle and the x- and y-axis coordinates reported by the mouse-click event message.
void CoordCheckMap( HWND hwnd, WORD xCoord, WORD yCoord )
{
BOOL Done = FALSE, Reverse;
HDC hdc;
WORD i;
int j, k, x, y;
...
randomize();
hdc = GetDC( hwnd );
x = random(3)-1;
y = random(3)-1;Initially, CoordMapCheck retrieves the device-context handle for the window displaying the map and selects step directions (x,y) in the range –1 to 1. Since these are used to increment the xCoord and yCoord values, the result is a search track beginning in one of eight compass directions (N, NE, E, SE, S, SW, W, NW).
NOTE
There is also one chance in nine that the initial search step will be (0,0), which is no search at all. This will, however, correct itself automatically when the next random search direction is selected.
Before the search is initiated, the first step is to check the present coordinates against a loop testing all of the identified coordinate pairs. Also, rather than requiring a perfect hit on the target coordinates, the actual test accepts any point that is within ten pixels of the target (total offset on both axes). As in a game of horseshoes, close does count. An exact match is not required, simplifying the search.
do
{
for( i=0; i<AllCoords; i++ )
{if( ( abs( xCoord - Coord[i].xPos ) +
abs( yCoord - Coord[i].yPos ) ) < 10 )
{
if( i < StateCoords )
LocationMsg( Coord[i].State );
else
PostMessage( hwnd, WM_COMMAND, IDM_MAP1, 0L );
Done = TRUE;
} }If the current coordinates are within a total of ten units of the target coordinates, a match is simply assumed. The hidden assumption here is that no target point is located within ten pixels of a border; otherwise, it could be misidentified by being detected from the wrong side of the border.
In other cases, a closer (or looser) match might be appropriate, so you would adjust the algorithm adjusted accordingly. For the present, a range of ten pixels is adequate for the purpose.
State coordinate pairs in the MapDemo demo are identified, together with the appropriate state names, as a simple structure table:
CoordState Coord[AllCoords] =
{ “Connecticut”, 267, 208, “Delaware”, 202, 311,
...
“Vermont”, 238, 132, “RETURN”, 14, 337,
“RETURN”, 331, 290, “RETURN”, 122, 81 };In addition to the state coordinates, the program provides three area coordinates that do not fall within a specific state: one below the upper New England states and two in the blank areas surrounding these states. Intersecting any of these three locations sends the application back to the USMAP01 display.
Alternatively, as long as a match is not found, the next test is to determine whether the bitmap borders have been reached:
Reverse = FALSE;
if( ( xCoord >= bmWidth-1 ) || ( xCoord <= 1 ) ||
( yCoord >= bmHeight-1 ) || ( yCoord <= 1 ) )
Reverse = TRUE;If the search is approaching the bitmap border, the Boolean Reverse flag is set and, subsequently, will reverse the search direction. Without this provision, the usual result under Windows will be a system application error, often trashing the system memory as well.
Next, as long as the search remains away from the bitmap border, a second loop executes a check of the immediate vicinity, searching for pixels identifying a border encounter and again reversing direction if a border is found.
else
for( j=-1; j<2; j++ )
for( k=-1; k<2; k++ )
if( GetPixel( hdc, xCoord+j, yCoord+k ) == BORDER )
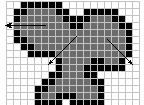
Reverse = TRUE;The program could have executed a simple, straight-ahead search, but this would have one fairly dangerous flaw: Narrow borders can leak through either single-pixel gaps or diagonal “pores,” both of which are illustrated in Figure 30.4.

Figure 30.4 Leaky borders using the drunkard’s walk algorithm
Here, a gap in the left border is one potential leak where a search trace could escape. Two other locations show pores where a diagonal search trace could escape. The remaining potential gaps in the original have been blocked in this version. Going through a bitmap looking for potential problems of this type is a tedious process and prone to error. Instead, the broad area-checking provisions in the preceding code accommodate a much less rigorous border condition.
Finally, if any of the preceding tests have set the Reverse flag, both the x and y increment variables are inverted by multiplying by –1.
if( Reverse )
{
x *= -1;
y *= -1;
}
else
if( ! random(10) )
{
x = random(3)-1;
y = random(3)-1;
}Alternatively, if no reverse condition has been encountered, a simple random test is used to change the search direction on a one-in-ten chance. Like the original one, the new search direction is selected randomly.
NOTE
A provision has been included in MapDemo to render the search trace visible by drawing a white dot at each step. This is implemented quite simply as: //=== option to trace random walk algorithm ========= SetPixel( hdc, xCoord, yCoord, 0x00FFFFFF );//===================================================To disable this trace provision, simply comment out this line of code.
Last, the current x and y incremental values are added to the xCoord and yCoord values before the do...while loop continues.
xCoord += x;
yCoord += y;
}
while( ! Done );
...
return;
}Figure 30.5 shows several drunkard’s walk searches executed in various New England states. The illustration was created by having the search paint its own trail markers. After the screen image was captured, the fill colors for each state were replaced by white, and the target points, which appear as small red dots in the map image, were replaced by asterisks for easier identification.
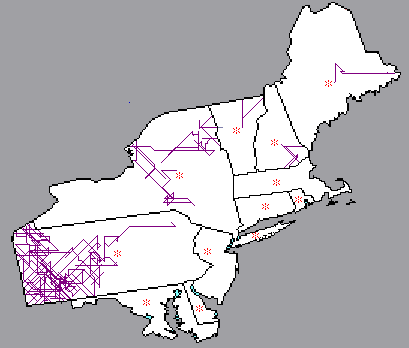
Figure 30.5: Drunkard’s walk searches in New England
As you can readily see in the traces in Figure 30.5, the drunkard’s walk algorithm is not the most efficient search method. Furthermore, as previously mentioned, there are times when this method is indeed ineffective.
For example, Figure 30.6 shows an enlargement of the search executed in Pennsylvania, with a circle added both to make the target region more visible and to show the nominal target radius. The search shown begins in the northeastern portion of the state, then passes relatively close to the target location, but not quite close enough to trigger a match, before executing a rather massive search of the western region and, finally, returning to the central region to find the target coordinates. On the other hand, since even a complex search like this executed in a matter of a less than a second, the inefficiency involved was relatively minor.
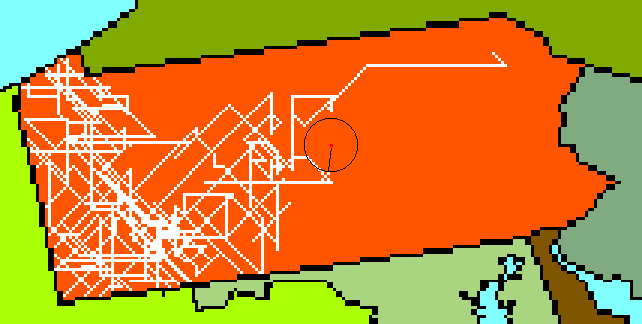
Figure 30.6: Searching Pennsylvania
Also, there are two factors that tend to mask these potential inefficiencies in the algorithm:
A third guard can be provided by selecting extra coordinate points within such regions. For an example, see the provisions for New York and Long Island in the MapDemo demo. (On the map, the island of Long Island is separate from the remainder of the state and has its own target coordinates.)NOTE
The drunkard’s walk algorithm is not without an occasional shortcoming. Stuart Ozer, who was my technical reviewer for the Windows 3.1 version of an earlier volume, reported finding a starting point on Cape Cod from which the algorithm required ten minutes or more to identify Massachusetts. Such a flaw could be blamed on the geometry of the search versus the boundary configuration, or it could be simply bad luck in the pseudo-random number sequence directing the search.