An algorithm that is particularly useful for identifying irregular regions is the drunkardís walk algorithm, titled thus because the search pattern follows a trace reminiscent of an inebriated and staggering pedestrian. (This type of motion is also known as Brownian motion, as exhibited by microscopic particles subject to thermal agitation.)
Where a drunkardóor a microscopic particleósimply continues indefinitely, the drunkardís walk algorithm executes a test after each staggering step (rather like a drunkard searching for any lamppost in reach) to determine if it has reached an identifiable point, and halts when such an encounter occurs. These target points are assigned locations within each enclosed region and are indexed to uniquely identify the region.
The drunkardís walk algorithm begins at a point indicated by the mouse click and proceeds in any arbitrary direction until one of these events occurs:
In the first case, reaching a boundary identified either by a change in color (or in the MapDemo demo, by a specific, preselected border color), the drunkardís path simply bounces or reverses. The drunkard then retraces its path until the second instance, a random change, forces a new direction or until, ultimately, the path intersects an identifiable point.
In the second case, a pseudo-random generator initiates a change in direction, on average every ten steps. Although in one chance out of eight, this chance is not a change at all, the overall effect is to trace paths with an average length of ten steps (or, in this case, pixels) between changes in direction.
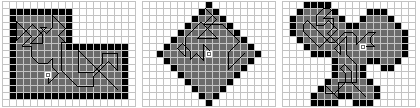
The third case is illustrated in Figure 30.3. This figure shows the same three regions illustrated in Figure 30.1, but this time with a drunkardís walk trace, which ends by intersecting the desired target coordinates (shown as a small box outline).

Figure 30.3: The drunkardís walk search