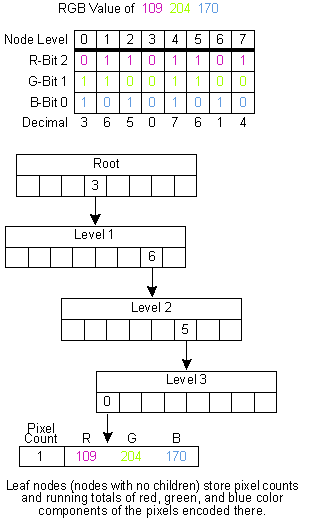
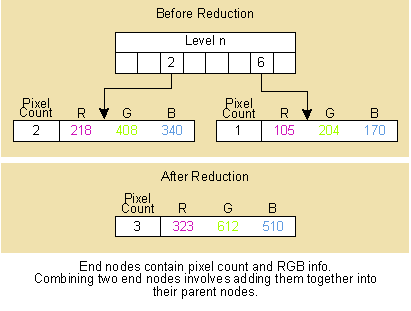
Jeff Prosise writes extensively about programming in Windows and is a contributing editor of several computer magazines. He is the author of Programming Windows 95 with MFC (Microsoft Press).

Psst! Want to see some wicked code?

This month marks the start of a new column in MSJ-one whose mission is to tackle sticky Win32¨ programming problems and present truly wicked solutions. Each column will come with the source code for a set of C-style procedures or C++ classes that you can download and use in your own applications. The aim is both to prevent you from having to duplicate the efforts of other programmers and to demonstrate effective Win32 programming techniques.

The subject of this month's column is color quantization using the Gervautz-Purgathofer octree method. (How's that for a mouthful?) Color quantization is the process of finding the optimal n colors with which to display a bitmap that contains m colors, where m is greater (usually much greater) than n. A quantized color palette enables bitmaps containing thousands or even millions of different colors to be displayed with reasonable accuracy on systems using 256-color video drivers. Scanning a bitmap and deciding which n colors best represents it in a logical color palette is not a trivial task. I'll make it easier for you by presenting a CreateOctreePalette function that takes a DIB section handle and gives you an HPALETTE in return. The algorithm this function uses is fast and requires substantially less memory than other color quantization algorithms. That, combined with the fact that it works equally well with 16, 24, and 32-bit DIB sections, makes CreateOctreePalette a handy addition to the toolbox of any Win32 graphics programmer.

Color Quantization Overview

Before I start slinging code, let's briefly discuss color quantization and why it's needed in Win32. Windows¨ uses a 24-bit RGB color model that represents individual colors by combining 8-bit red, green, and blue values. On video adapters that support 24-bit color, Windows displays colors on the screen exactly as you specify them. On palettized output devices, Windows maps RGB color values to the nearest colors in the system palette. The vast majority of palettized video adapters can display at most 256 colors at a time. When a 24-bit bitmap is displayed on a 256-color device with the default system palette, colors in the bitmap are mapped to the same 20 static colors that the GDI programs into the adapter's palette registers for menus, window frames, and so on. The resulting image typically suffers severe color degradation due to the limited number of colors available.

The display quality of 24-bit images can be vastly improved by creating a logical palette that contains up to 236 colors and realizing the palette prior to displaying the image. You want 236 colors (instead of 256) because the top 10 and bottom 10 color-palette entries are those static colors mentioned previously. The trick, of course, is picking the right 236 palette colors. Choose your colors wisely and most 24-bit images will look almost as good on 256-color screens as they do on 16.7 million-color screens. (Dithering can further improve the quality of the output, but that's a topic for another day.) Choose them poorly, and the resulting image won't look much better on a 256-color screen than it would on a 16-color VGA screen.

There are two basic approaches to picking palette colors for images containing thousands of different colors: you can create a generic halftone palette containing a rainbow of colors, or you can create a quantized palette containing colors derived from those in the image. The first approach is simpler and faster because the palette colors can be picked without regard to the image colors. With Win32, you can create a halftone palette in one line of code by calling the CreateHalftonePalette API function. In 256-color environments, CreateHalftonePalette returns an HPALETTE referencing a palette that includes the 216 colors in a 6 ´ 6 ´ 6 color cube plus a variety of handpicked colors useful for grayscale imaging and other applications. The wide distribution of colors in a halftone palette ensures that no color in the image will undergo a wholesale color shift. On the downside, subtle variations in tone will be lost.

A quantized palette (also known as an "adaptive" or "optimized" palette) generally produces a markedly better image than a halftone palette because the colors in the palette are driven by the colors in the image. Think of it this way: displaying a picture of a red ball containing 200 different shades of red essentially wastes all the halftone palette colors with nonzero blue or green components. Displaying the same image with a quantized palette yields more accurate results because the preponderance of reds in the image produces a similar bias toward red in the quantized palette colors.

How do you pick 236 palette colors to represent an image that contains a much wider variety of colors? In the past, programmers have favored two techniques. The "popularity method" counts the number of occurrences of each color in the image and assigns the most frequently occurring colors to the palette. In the median-cut method, a 3D cube representing RGB color space is recursively subdivided until it has been carved into volumes representing roughly equal numbers of pixels. Palette colors are chosen by averaging the RGB color values of the pixels in each volume or simply computing each volume's centroid.

The popularity method is simpler to implement in code. The usual approach is to create an array representing a histogram of colors and color frequencies, sort the array in order of descending frequencies, and copy the first 236 colors in the array to the palette. To keep the array size manageable, the least significant 3 or 4 bits of each 8-bit color component are normally discarded. A popularity palette generally produces better output than a halftone palette, but infrequently appearing colors that are nonetheless important to the eye may be omitted.

The widely used algorithm for median-cut color quantization developed in the early 1980s by Paul Heckbert overcomes many deficiencies of the popularity method. Heckbert's algorithm has been documented and analyzed in countless papers, books, and magazine articles so I won't rehash the details here. This method produces a highly optimized palette that is finely tuned to the colors in the image. Unfortunately, practical implementations of the algorithm require generous amounts of memory, and there is inevitably some sorting to be done on large arrays.

Octree Color Quantization

In 1988, M. Gervautz and W. Purgathofer of Austria's Technische UniversitŠt Wien published an article entitled "A Simple Method for Color Quantization: Octree Quantization." They proposed an elegant new method for quantizing color bitmap images by employing octrees-tree-like data structures whose nodes contain pointers to up to eight subnodes. Properly implemented, octree color quantization is at least as fast as the median-cut method and more memory-efficient.

The basic idea in octree color quantization is to graph an image's RGB color values in a hierarchical octree. The octree can go up to nine levels deep-a root level plus one level for each bit in an 8-bit red, green, or blue value-but it's typically restricted to fewer levels to conserve memory. Lower levels correspond to less significant bits in RGB color values, so allowing the octree to grow deeper than five or six levels has little or no effect on the output. Leaf nodes (nodes with no children) store pixel counts and running totals of the red, green, and blue color components of the pixels encoded there, while intermediate nodes form paths from the topmost level in the octree to the leaves. This is an efficient way to count colors and the number of occurrences of each color because no memory is allocated for colors that don't appear in the image. If the number of leaf nodes happens to be equal to or less than the number of palette colors you want, you can fill a palette simply by traversing the octree and copying RGB values from its leaves.

The beauty of the octree method is what happens when the number of leaf nodes n exceeds the desired number of palette colors k. Each time adding a color to the octree creates a new leaf, n is compared to k. If n is greater than k, the tree is reduced by merging one or more leaf nodes into the parent. After the operation is complete, the parent, which was an intermediate node, is a leaf node that stores the combined color information of all its former children.

Because the octree is trimmed continually to keep the leaf count under k, you end up with an octree containing k or fewer leaves whose RGB values make ideal palette colors. No matter how many colors the image contains, you can walk the octree and pick leaves off it to formulate a palette. Better yet, the octree never requires memory for more than k+1 leaf nodes plus some number of intermediate nodes.

There are two parts of an octree that I want to study: the parent-child relationship between nodes and the significance of the RGB data in each leaf. Figure 1 shows the parent-child relationship for each node. At a given level in the tree, a value from zero to 7, derived from the RGB color value, identifies a child node. At the uppermost (root) level, bit 7 of the red value is combined with bit 7 of the green value and bit 7 of the blue value to form a 3-bit index. Bit 7 from the red value becomes bit 2 in the index, bit 7 from the green value becomes bit 1 in the index, and bit 7 from the blue value becomes bit zero in the index. At the next level, bit 6 is used instead of bit 7, and the bit number keeps decreasing as the level number increases. For red, green, and blue color values equal to 109 (binary 01101101), 204 (11001100), and 170 (10101010), the index of the first child node is 3 (011), the index of the second child node is 6 (110), and so on. This mechanism places the more significant bits of the RGB values at the top of the tree. In this example, the octree's depth is restricted to five levels, which allows you to factor in up to 4 bits of each 8-bit color component. The remaining bits are effectively averaged together.

Figure 1 How an Octree Maps RGB Values

To help you visualize how RGB values and pixel counts are stored in octree leaves, Figure 2 depicts part of an octree that charts one occurrence of the color RGB (105, 204, 170) and two occurrences of RGB (109, 204, 170) both before and after reduction. The RGB value is multiplied by the number of pixels containing that value and the result is stored in the leaf. Before reduction, the octree contains two leaves-one for each color. After reduction, it contains one. Dividing the combined red, green, and blue values in the leaves before reduction by the combined number of pixels represented (3) yields an average color value of RGB (107, 204, 170). This value is multiplied by the number of pixels represented and stored in the reduced node.

Figure 2 Reducing Two Leaves of an Octree

The Code

The source code shown in Figure 3 is the complete listing for an app named Colors that loads and displays BMP files. Commands in the Options menu let you choose from three methods of palette formation, and depth of the octree. No Palette displays bitmaps with the default system palette; Halftone Palette uses a halftone palette created by the CreateHalftonePalette API function; and Optimized Palette uses a palette of matching colors for bitmaps with up to 8 bits of color information per pixel and a quantized palette for bitmaps featuring 16, 24, or 32 color bits per pixel. Quantized color palettes are created through the Gervautz-Pergathofer octree method. Palettes are not used on video adapters that display 16 or 24-bit color, so to see the differences in the output be sure to switch your display settings to a 256-color video mode.

Figure 4 shows a 24-bit color image in its original form. Figures 5, 6, and 7 show the same image displayed on a 256-color screen with the three palette options. The No Palette method (see Figure 5) is the worst of the three because the 20 static colors in the default system palette simply don't provide the variety of colors needed to accurately portray the image. Halftone Palette is better (see Figure 6), but even it exhibits pronounced posterization effects. The octree version created with Optimized Palette (see Figure 7) is almost as good as the original; in fact, the two are virtually identical on a four-color magazine page. These examples illustrate the dramatic difference color selection can make on palettized video adapters.

Figure 4 Original 24-bit image

Figure 5 Default system palette

Figure 6 Halftone palette

Figure 7 Octree palette

The quantization code is found in the CreateOctreePalette function and its helpers. As a group, the functions are self-contained; all you have to do to import them into your own code is cut and paste the CreateOctreePalette, AddColor, CreateNode, ReduceTree, DeleteTree, GetPaletteColors, GetRightShiftCount, and GetLeftShiftCount functions and their corresponding function prototypes.

You'll also need to supply a value to the nColorBits parameter, which controls the depth of the tree by specifying the number of significant bits in each 8-bit color component. This value can be from 1 to 8 (higher numbers give better quality and use more memory), but you will find that a value of 4 or 5 provides the best compromise of performance and memory use. If you want to see the effects of the other values, try them in the sample program.

To use these functions, simply pass CreateOctreePalette a handle to a DIB section (DDBs and ordinary DIBs won't do) and a value specifying the maximum number of colors in the palette. Then select the returned HPALETTE into a device context and realize it before displaying the image. It's your responsibility to delete the HPALETTE when you're through with it. Note that the palette CreateOctreePalette creates will sometimes contain slightly fewer colors than the number you specify. A reduction in the octree size lops off up to seven leaves, so there's no guarantee the final octree will contain exactly nMaxColors colors.

There's a lot that goes on behind the scenes when you call CreateOctreePalette. The important part is that CreateOctreePalette scans the bitmap pixel by pixel and passes the RGB color of each pixel to AddColors. AddColors calls itself recursively to add octree nodes or add color information to existing nodes. Each node in the octree is represented by a structure of type NODE, which is defined in Colors.h. Memory for each node is allocated and initialized by the CreateNode function. After adding a color to the octree, CreateOctreePalette compares the number of leaves (nLeafCount) to nMaxColors and calls ReduceTree if the leaf count needs to be reduced. After the entire bitmap is scanned, GetPaletteColors traverses the octree from top to bottom copying leaf colors to a LOGPALETTE structure, then calls CreatePalette to create the logical palette. Before returning, CreateOctreePalette calls the recursive DeleteTree function to free memory allocated to the octree nodes.

One implementation detail you should be aware of, especially if you want to modify the code, is how ReduceTree picks a node to reduce. It's important to do your reductions as deep in the octree as possible because deeper levels correspond to subtler variations in tone. Since it's time-consuming to traverse the entire tree from top to bottom, I borrowed an idea from an excellent article by Dean Clark that appeared in the January 1996 issue of Dr. Dobb's Journal ("Color Quantization Using Octrees"); I implemented an array of linked lists named pReducibleNodes containing pointers to all the reducible (non-leaf) nodes in each level of the octree. Thus, finding the deepest level with a reducible node is as simple as scanning the array from bottom to top until a non-NULL pointer is located. Like Dean's code, mine picks the node most recently added to a given level as the one to reduce. You could refine my implementation somewhat by adding more intelligence to the node-selection process-for example, by walking the linked list and picking the node that represents the fewest or the most colors.

Colors uses the versatile LoadImage function in Windows 95 to create a DIB section from a BMP file with one function call. It features a handy CreateExactPalette function for creating a palette of matching colors for 1, 4, and 8-bit images, and it demonstrates how to extract color information from raw bitmap bits in 16, 24, and 32-bit images. For details, see the code following the case statements in CreateOctreePalette.

Your Needs, Your Ideas

That's it for this month. Meanwhile, if there are tough Win32 questions you'd like to see answered, send me e-mail at the address listed below. I regret that time doesn't permit me to respond individually to all messages, but rest assured that I'll read every suggestion and consider each for inclusion in a future column.

Have a tricky issue dealing with Windows? Send your questions via e-mail to Jeff Prosise: 72241.44@compuserve.com