Algorithms

Stacks and Queues

An Introduction to LIFOs, FIFOs, and Heaps

By Rod Stephens

You might think holding a list of items would be easy. Just stick them in an array, and off you go to the driving range. Arrays work for some lists, but depending on the kinds of operations you'll need to perform on the items, other data structures are sometimes better.

This article explains two special kinds of lists: stacks and queues. It also describes priority queues and explains two ways you can implement them in VBA.

Stacks

A stack is a list where items are added to one end of the list and removed from the same end. Whatever goes on to the list last comes out first. Because the items are removed in last-in-first-out order, stacks are also sometimes called LIFO lists, or LIFOs. For historical reasons, adding an item is called pushing the item onto the stack; removing an item is called popping it off the stack.

You can think of a stack as a stack of items on a desk. You can add items at the top of the stack and remove them from the top, but if you try to pull an item from the middle, the stack falls over and makes a mess on your floor.

You can build a simple stack using a Collection object. Use the Collection's Add method to push an item onto the stack. Use the Remove method to remove the most recently added item from the stack. FIGURE 1 shows how you could build a simple Collection-based stack in VBA.

Option Explicit

' The stack items.

Private TheStack As Collection

' Create the stack Collection.

Private Sub UserForm_Initialize()

   Set TheStack = 
      New Collection

End Sub

' Push an item onto the stack.

Private Sub cmdPush_Click()

   ' Add the value to the stack.

  TheStack.Add txtValue.Text

   ' Blank the value.

  txtValue.Text = ""

End Sub

' Pop an item off the stack.

Private Sub cmdPop_Click()

   ' Display the last value.

  txtValue.Text = TheStack(TheStack.Count)

   ' Remove the last value.

  TheStack.Remove TheStack.Count

End Sub

FIGURE 1: Implementing a stack using a Collection.

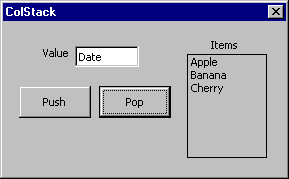
The ColStack UserForm shown in FIGURE 2 uses this strategy to implement a stack (all example forms and source code discussed in this article are available for download; see end of article for details). Enter a value and click the Push button to add the value to the stack. Click the Pop button to remove the last item from the stack. (Note: This program performs no error checking, so if you try to pop an item while the stack is empty, the program crashes.)

FIGURE 2: The ColStack UserForm uses a Collection to implement a stack.

The previous code is relatively straightforward, but it ties the main program closely to the stack Collection. While not a big deal here, this sort of close connection is generally a bad idea. If you later decide to change the way the stack is stored, you will need to modify the main program. If the program uses several stacks, the changes could get complicated.

To separate the program from the stack code, you can create a stack class. This class provides Push and Pop routines that the main program uses to manipulate the stack. Internally, the class can store the items in a Collection, or some other data structure. The main program does not need to know the details. Later, if you decide to re-implement using some other storage method, you don't need to modify the main program.

FIGURE 3 shows a stack class implemented using a Collection. This code is similar to the code shown in FIGURE 1.

Option Explicit

' The stack Collection.

Private Items As Collection

' Allocate the stack Collection.

Private Sub Class_Initialize()

   Set Items = New Collection

End Sub

' Push a value onto the stack.

Public Sub Push(ByVal value 
      As String)

  Items.Add value

End Sub

' Pop a value off of the stack.

Public Function Pop()As String

   ' Get the last value.

  Pop = Items(Items.Count)

   ' Remove the last value.

  Items.Remove Items.Count

End Function

FIGURE 3: A stack class.

FIGURE 4 shows how the frmStack UserForm demonstrates the stack class. It uses a Stack object's Push and Pop routines without knowing how the stack works.

Option Explicit

' The Stack object.

Private TheStack As Stack

' Create the Stack object.

Private Sub UserForm_Initialize()

   Set TheStack = 
      New Stack

End Sub

' Push an item onto the stack.

Private Sub cmdPush_Click()

   ' Add the value to the 
      stack.

  TheStack.Push txtValue.Text

   ' Blank the value.

  txtValue.Text = ""

End Sub

' Pop an item off the stack.

Private Sub cmdPop_Click()

   ' Display the last value.

  txtValue.Text = TheStack.Pop()

End Sub

FIGURE 4: Using the stack class.

Once the main program is separated from the stack implementation, changing how the stack works is easy. The ArrayStack class shown in FIGURE 5 manages a stack with an array instead of a Collection. This version uses a simple resizing strategy. Whenever the item array is full, the program increases its size by 10 items. A more sophisticated approach might add a percentage of the array's current size to reduce the number of times the array is resized when it is very large. A more advanced version could also shrink the array when it contained too many unused entries.

Option Explicit

' The stack Collection.

Private Items()As String

Private NumAllocated As Integer

Private NumUsed As Integer

' Push a value onto the stack.

Public Sub Push(ByVal value 
      As String)

   ' Make sure there is room 
      for the item.

  NumUsed = NumUsed + 1

   If NumUsed > 
      NumAllocated Then

    NumAllocated = NumAllocated + 10

     ReDim 
      Preserve Items(1 To NumAllocated)

   End If

   ' Add the item to the 
      array.

  Items(NumUsed) = value

End Sub

' Pop a value off of the stack.

Public Function Pop()As String

   ' Get the last value.

  Pop = Items(NumUsed)

   ' Remove the last value.

  NumUsed = NumUsed - 1

End Function

FIGURE 5: An array-based stack class.

The frmArrayStack UserForm also demonstrates the ArrayStack class. This program differs from frmStack in only the two lines where the stack object is declared and initialized:

Private TheStack As ArrayStack

...

   Set TheStack = 
      New ArrayStack

Queues

A queue is another specialized list where items are added at one end of the list and removed from the other. The first item in is the first item out. Because the items are removed from a queue in first-in-first-out order, stacks are also sometimes called FIFO lists, or FIFOs.

Just as you can use a Collection to build a stack, you can use a Collection to build a queue. The only difference is in how you remove items from the queue. Instead of removing the Collection's last item, you remove the first.

You can also insulate the main program from the details of the queue implementation using a class. FIGURE 6 shows a queue class that implements a queue using a Collection. The frmQueue UserForm demonstrates this class.

Option Explicit

' The queue Collection.

Private Items As Collection

' Allocate the queue Collection.

Private Sub Class_Initialize()

   Set Items = New Collection

End Sub

' Add a value to the queue.

Public Sub Enter(ByVal value 
      As String)

  Items.Add value

End Sub

' Remove the first item from the queue.

Public Function Leave()As String

   ' Get the first value.

  Leave = Items(1)

   ' Remove the first value.

  Items.Remove 1

End Function

FIGURE 6: A Collection-based queue class.

Building a queue with an array is much harder than building a stack with an array. The problem is that the bottom of the queue doesn't stay in one place. If you remove an item from the natural array implementation, the index of the oldest item in the queue increases. As you add and remove more items, the indexes of the items in use can grow quite large. The beginning of the array ends up holding a lot of entries that are no longer used.

One way to build a more efficient array-based queue is to use modular arithmetic. When you fill the array, you start adding items again at the beginning. This data structure is called a circular queue because it works as if the array were bent in a circle with the end attached to the beginning. I'll leave as an exercise the details of what to do when the array is completely full.

Priority Queues

An interesting variety of queue is the priority queue. In a priority queue, each item has an associated priority. Items are added to the queue as usual, but they are removed in order of their priorities. At any moment, the queue must be able to find and remove its highest priority item.

There are many ways you can implement a priority queue. For example, you could add new items to the end of an array or Collection. To remove an item, you would examine all the items to find the one with the highest priority.

The PQueue class shown in FIGURE 7 uses two Collections, one for values and one for priorities, to implement this kind of priority queue. The frmPQueue UserForm demonstrates this class (see FIGURE 8). Enter a value and a priority and click the Enter button to add the value to the queue. Click the Leave button to remove the highest priority item from the queue.

Option Explicit

' The item Collection.

Private Items As Collection

' The priority Collection.

Private Priorities As Collection

' Allocate the Collections.

Private Sub Class_Initialize()

   Set Items = New Collection

   Set Priorities = 
      New Collection

End Sub

' Add a value to the queue.

Public Sub Enter(ByVal value 
      As String, _

ByVal priority As Integer)

  Items.Add value

  Priorities.Add priority

End Sub

' Remove the highest priority item from 
      the queue.

Public Sub Leave(ByRef value 
      As String, _

ByRef priority As Integer)

  Dim i As Integer

  Dim best_i As Integer

  Dim best_priority 
      As Integer

   ' Find the highest priority 
      item.

  best_i = 1

  best_priority = Priorities(1)

   For i = 2 To Priorities.Count

     If 
      best_priority < Priorities(i) Then

      best_priority = 
      Priorities(i)

      best_i = i

     End 
      If

   Next i

   ' Set the return values.

  priority = best_priority

  value = Items(best_i)

   ' Remove this value.

  Items.Remove best_i

  Priorities.Remove best_i

End Sub

FIGURE 7: The PQueue class uses two Collections to implement a priority queue.

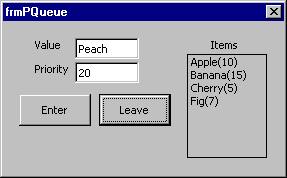
FIGURE 8: The frmPQueue UserForm uses a Heap object to manage a priority queue.

Heaps

For small queues, the PQueue class is effective. For larger queues, searching the entire list of items to find the one with the highest priority is unnecessarily slow. You can make a much more efficient priority queue using a data structure called a heap.

A heap is a complete binary tree where every node in the tree is at least as large as its children. Note that either child could be larger than the other, as long as both are smaller than their parent (so this is not a completely sorted tree). FIGURE 9 shows a heap.

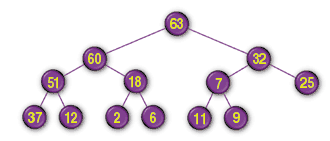
FIGURE 9: A heap.

Because a heap is a complete binary tree, you can store it compactly in an array. Place the root of the tree in array position 1. For the node in position I, put its children in positions 2 * I and 2 * I + 1. For example, the children of the node in position 3 are in positions 2 * 3 = 6 and 2 * 3 + 1 = 7. FIGURE 10 shows the heap in FIGURE 9 stored in an array. You can verify in FIGURES 9 and 10 that the value 25 stored in position 3 has children with values 7 and 12 stored in positions 6 and 7.

FIGURE 10: The heap from FIGURE 9 stored in an array.

The reason heaps are mentioned here is that they make excellent priority queues. If the items' priorities are used to arrange the heap, the item with the highest priority is always at the root of the tree. That makes finding the highest priority item a snap. The hard part is in making the tree a heap when you add and remove items.

To add a new item, the program puts the item in the heap array just after the current last item. FIGURE 11 shows the heap from FIGURE 9 with the new value 32 added at the end.

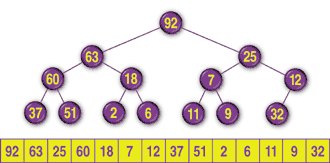
FIGURE 11: The heap from FIGURE 9 with a new item added.

Unfortunately, the tree is no longer a heap because the new item has a value greater than its parent's. To turn the tree back into a heap, the program compares the new item with its parent. If the child is larger, the program swaps the two items.

Note that the parent's other child, if it has one, is smaller than the parent because the tree was a heap before we added the new item. If the new item is larger than the parent, it must also be larger than the other child. That means moving the new item into the parent's position is OK, at least locally. The new item is larger than both of its children in the new position.

Next, the program compares the new item to its parent in its new position. If the new item is larger, the program swaps those two items. The program continues pushing the new item up through the tree until it finds a parent that is larger or it has reached the root. At that point the tree is once again a heap. In this example, the value 32 is swapped upward twice to give the tree shown in FIGURE 12.

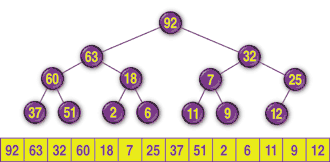
FIGURE 12: The tree turned back into a heap.

To remove the highest priority item from the heap, the priority queue simply removes the root item. This creates a rootless data structure that is not even a tree, much less a heap.

To rebuild the heap again, the program moves the last item in the tree into the top position. This doesn't give a heap, but at least the data structure is a tree again. Performing these steps for the tree shown in FIGURE 12 gives the new tree in FIGURE 13.

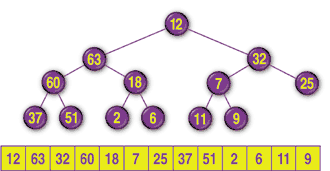
FIGURE 13: The tree after replacing its top item with its bottom item.

To turn the tree back into a heap, the program compares the new root value with its children. If one of the children is larger, the program swaps the new value with its larger child. That gives the tree the heap property at this node. In this example, the program swaps the value 12 with the value 63.

The program then compares the new value to its children in its new position. If one of the children has a larger value, the program swaps the new value with its larger child. The program continues pushing the new value down into the tree until it reaches a point where it is larger than both of its children or it reaches the bottom of the tree. At this point, the tree is again a heap. Performing these swaps for the tree in FIGURE 13 gives the heap shown in FIGURE 14.

FIGURE 14: The tree is once again a heap after removing its top-most item.

The Heap class, shown in Listing One, uses these heap operations to maintain a priority queue. Items in the queue are stored in an array of the ValueInfo user-defined type. The class uses the type's priority field to order the heap. It uses the HeapPushUp and HeapPushDown subroutines to rebuild the heap when new items are added or removed. These routines make the Enter and Leave subroutine relatively straightforward.

Heap Performance

The HeapPushUp and HeapPushDown subroutines are more complicated than the simple search used by the PQueue class, but they are much faster for large queues.

To insert an item in its Collection, the PQueue class only needs to execute a few steps. To find the item with the highest priority, however, PQueue must examine every item in the queue. If there are N items in the queue, that takes on the order of N steps.

On the other hand, to add a new item to its heap, the Heap class may need to push the new item from the bottom of the heap all the way to the top. If there are N items in the queue, the tree is roughly Log₂(N) levels tall - so that can take at most Log₂ (N) steps. Similarly, when the Heap class removes its highest priority item, it may have to push a new item from the top of the tree to the bottom. That can also take at most Log₂ (N) steps.

For very large priority queues, the 2 * Log₂ (N) steps used by the Heap class is faster than the N steps used by the PQueue class. For instance, if there are 1,000 items in the queue, the PQueue class will need roughly 1,000 steps to find and remove the highest priority item, while the Heap class will need only Log₂ (1000) = 10 steps to rebuild its heap. If the queue contains one million items, the PQueue class will need one million steps to find the highest priority item, while the Heap class will need only around Log₂ (1000000) = 20.

Conclusion

Stacks, queues, and priority queues are useful in many algorithms. Using Collections, arrays, and heaps, you can strike a balance between performance and complexity. Package these data structures in classes to insulate your programs from the implementation details. Then you can use the most appropriate method without forcing a major rewrite of your projects.

The examples referenced in this article are available for download.

Rod's book Ready-to-Run Visual Basic Algorithms, Second Edition has a lot more to say about stacks, queues, and other useful data structures. Learn more about his books or download some of his example programs at http://www.vb-helper.com/">http://www.vb-helper.com/. You can contact Rod via e-mail at mailto:RodStephens@vb-helper.com.

Begin Listing One - The Heap class

Option Explicit

' Data type to hold values and 
      priorities.

Private Type ValueInfo

  value As String

  priority As Integer

End Type

' The item array.

Private Items()As ValueInfo

Private NumItems As Integer

Private NumAllocated As Integer

' Push the item in position min down 
      into the

' tree until its children are larger 
      than it is.

Private Sub HeapPushDown(ByVal 
      min As Integer, 
      _

ByVal max As Integer)

  Dim tmp As ValueInfo

  Dim j As Integer

Do

     ' Examine the 
      children of min.

    j = 2 * min

     ' See if we 
      have dropped off the tree.

     If j 
      <= max Then

       ' 
      We have not. Make j point to the child

       ' 
      with the higher priority.

       
      If j < max Then

         If Items(i + 1).priority > Items(j).priority 
      Then

' The other child has a higher priority.

j = j + 1

         End If

       
      End If

       ' 
      Compare the min and j entries.

       
      If Items(j).priority <= Items(min).priority Then

         ' The min item is already larger than

         ' its children. We're done.

         Exit Do

       
      Else

         ' The min item is smaller than the j item.

        ' Swap them.

        tmp = 
      Items(min)

        Items(min) = 
      Items(j)

        Items(j) = 
      tmp

         ' Continue pushing from this position.

        min = j

       
      End If

     End 
      If

   Loop

End Sub

' Push the last item up through the heap 
      until

' until it is larger than its children.

Private Sub HeapPushUp(ByVal max 
      As Integer)

  Dim tmp As ValueInfo

  Dim j As Integer

Do

     ' Find the 
      parent of max.

    j = max \ 2

     ' See if we 
      have reached the top.

     If j 
      < 1 Then Exit 
      Do

     ' Compare the j 
      entry to the max entry.

     If 
      Items(j).priority < Items(max).priority Then

       ' 
      The parent is smaller. Swap them.

      tmp = Items(j)

      Items(j) = 
Items(max)

      Items(max) = tmp

       ' 
      Continue pushing from this position.

      max = j

     End 
      If

   Loop

End Sub

' Add a value to the heap.

Public Sub Enter(ByVal value 
      As String, _

ByVal priority As Integer)

   ' Make sure there is room 
      for the new item.

  NumItems = NumItems + 1

   If NumItems > 
      NumAllocated Then

    NumAllocated = NumAllocated + 10

     ReDim 
      Preserve Items(1 To NumAllocated)

   End If

   ' Add the new item.

   With 
      Items(NumItems)

    .priority = priority

    .value = value

   End With

   ' Make the array a heap 
      again.

  HeapPushUp NumItems

End Sub

' Remove the highest priority item from 
      the queue.

Public Sub Leave(ByRef value 
      As String, _

ByRef priority As Integer)

   ' Return the top item.

   With Items(1)

    value = .value

    priority = .priority

   End With

   ' Move the last item to the 
      top.

  Items(1) = Items(NumItems)

  NumItems = NumItems - 1

   ' Push this item down into 
      the tree until

   ' we have a heap again.

  HeapPushDown 1, NumItems

End Sub

End Listing One