By Rod Stephens
In nature, a tree is something from which you can hang your hammock. In programming, a tree is a data structure that stores objects in a hierarchical arrangement. Company organizational charts, multi-level menus, and directory structures are naturally hierarchical and easy to store and manipulate using trees.
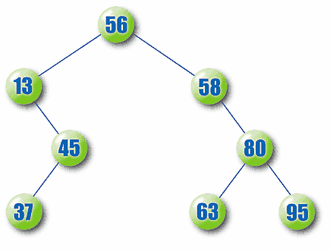
Tree TermsBefore you begin a serious study of trees, you should know some basic tree terminology. You can define a tree recursively as a data structure with a root node connected to zero or more subtrees. Trees are customarily drawn with the root node at the top, as shown in Figure 1. The tree in Figure 1 contains a root node labeled A, connected to two subtrees with roots B and C. The subtree with root B has a root node (B) connected to two subtrees with roots D and E. The trivial trees with roots C, D, and E are connected to no subtrees.
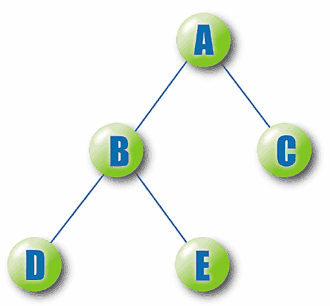
Figure 1: A Tree
The nodes in a tree are connected by links or branches. Each branch defines a parent-child relationship between the two nodes it connects. The upper node is the parent, and the lower node is the child.
The nodes along the path from a node to the root are the node’s ancestors. Conversely, if a node is another’s ancestor, that node is the ancestor’s descendant. For example, in Figure 1, nodes A and B are ancestors of node E. Nodes D and E are the descendants of node B.
The degree of a node is the number of children it has. The degree of the tree is the largest degree of any node.
Trees of degree 2 are called binary trees, and trees of degree 3 are sometimes called ternary trees. A leaf is a node with degree 0 (like nodes C, D, and E). All other nodes are called internal nodes.
A node’s height or depth in the tree is 1 plus the number of its ancestors. The height of the tree is the largest of the nodes’ heights. The tree in Figure 1 has degree 2 (nodes A and B each have two children) and height 3 (nodes D and E have height 3).
As you can see, tree terminology is a mishmash of words stolen from genealogy (parent, child, ancestor) and botany (branch, node, leaf).
Building TreesIn Visual J++, you can build a tree using a node class. This class should define public variables to represent the node’s value and links to its children. The following code shows how a program might define a BinaryNode class. It defines a string data value and two references to child nodes:
// A binary node class.
private class BinaryNode
{
public String NodeValue;
public BinaryNode LeftChild;
public BinaryNode RightChild;
}Using the BinaryNode class, a program can build a small tree. Figure 2 shows code that builds a tree similar to the one shown in Figure 1.
// Make a tree like the one in
Figure 1.
private BinaryNode MakeTree()
{
BinaryNode root, child;
// Create the root node A.
root = new BinaryNode();
root.NodeValue = "A";
// Create node B.
child = new BinaryNode();
child.NodeValue = "B";
root.LeftChild = child;
// Create node C.
child = new BinaryNode();
child.NodeValue = "C";
root.RightChild = child;
// Create node D.
child = new BinaryNode();
child.NodeValue = "D";
root.LeftChild.LeftChild = child;
// Create node E.
child = new BinaryNode();
child.NodeValue = "E";
root.LeftChild.RightChild = child;
return root;
}
Figure 2: Code that builds the binary tree shown in Figure 1.
To build a tree of higher degree, you can add more child references to the node class. For example, you might define a node for a ternary tree like this:
// A ternary node class.
private class TernaryNode
{
public String NodeValue;
public BinaryNode LeftChild;
public BinaryNode MiddleChild;
public BinaryNode RightChild;
}For trees of higher degree, using separate child variables is cumbersome. You can build a more flexible node class using an array to store each node’s children:
// A node of arbitrary degree.
private class TernaryNode
{
public String NodeValue;
public TernaryNode Children[];
}There are many kinds of trees with different degrees and management policies. One particularly useful variety is the sorted binary tree. In this kind of tree, items are arranged so each node’s value is greater than its left child’s, and smaller than its right child’s. Figure 3 shows a small sorted tree.

Figure 3: A sorted binary tree.
The example program SortTree, shown in Figure 4, allows you to create and study sorted binary trees. Enter integer values in the Value field and click the Add button to add a new value to the tree. Enter a value and click Find to find the value if it’s in the tree. The Preorder, Inorder, Postorder, and Breadth-First option buttons display the tree’s nodes in different orders, which I’ll describe shortly.
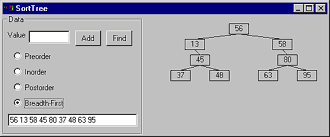
Figure 4: The SortTree program.
Program SortTree performs five main tasks:
Adding nodes to the tree
Finding nodes in the tree
Positioning nodes
Displaying nodes
Displaying the preorder, inorder, postorder, and breadth-first traversals
These tasks are described in the following sections.
Adding NodesWhen you need to add a node to a sorted tree, you cannot simply put it anywhere; it must be placed in the correct position to keep the tree sorted.
To add a node, the program begins at the tree’s root. It compares the new node’s value to the root’s value. If the new value is smaller, the program continues to search for the node’s location by examining the root’s left child. If the new value is larger than the root’s value, the program searches for the node’s location by examining the root’s right child.
The program continues searching down the tree until it reaches the bottom of the tree. Each time it examines a node, it compares the node’s value to the new value and follows the appropriate branch. When the program needs to examine a node that is not present, the program inserts the new node at that point.
For example, suppose you want to insert the value 48 in the tree shown in Figure 3. The program first compares 48 to the root node’s value, 56. Because 48 < 56, the program searches the root’s left child. It then compares 48 to 13. Because 48 > 13, the program examines that node’s right child and compares 48 to 45. Because 48 > 45, the program should next examine the node’s right child. In this case, there is no right child, so the program inserts the new node as the right child of the node containing 45. This gives the tree shown in Figure 5.
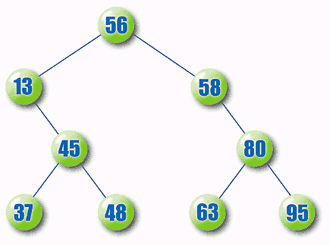
Figure 5: A sorted binary tree with the value 48 added.
A program can search through a tree using a variable to keep track of the node it is examining. Another approach is to make the tree’s nodes provide an InsertValue method. The InsertValue method inserts the new value in the correct position within the node object’s subtree.
Figure 6 shows the InsertValue subroutine a SortedNode class would use to insert a new value within its sorted subtree. The routine first compares the new value to the node’s value. If the new value is smaller, the routine examines the node’s left child. If that child is null, InsertValue creates a new left child for the node, and inserts the new value in it. If the left child isn’t null, InsertValue invokes the child’s InsertValue method to add the new value in the left child’s subtree.
// Insert a new value into the node's subtree.
public void InsertValue(int new_value)
{
if (new_value < NodeValue)
{
// Insert in the left subtree.
if (LeftChild == null)
{
// Insert the node here.
LeftChild = new SortedNode();
LeftChild.NodeValue = new_value;
}
else
{
// Make the left child insert the item
// in its subtree.
LeftChild.InsertValue(new_value);
}
}
else
{
// Insert in the right subtree.
if (RightChild == null)
{
// Insert the node here.
RightChild = new SortedNode();
RightChild.NodeValue = new_value;
}
else
{
// Make the right child insert the
// item in its subtree.
RightChild.InsertValue(new_value);
}
}
} // End InsertValue method.
Figure 6: Code that inserts a value in a sorted binary tree.
Inserting a value that is larger than the node’s value is similar, but it uses the node’s right child instead of its left child.
A program managing a sorted tree would invoke the root node’s InsertValue method to add a new value to the tree. Calls to InsertValue then move down through the nodes in the tree until they find the new item’s proper location.
This technique is common in tree operations. The main program invokes a method provided by the root node. The root either performs the task directly, or invokes a method of one of its children. The child then performs the task directly, or invokes a method of one of its children. The method calls continue to move down into the tree until they reach a node that can perform the desired operation.
Finding ItemsFinding a value in a sorted tree is similar to adding one. Starting at the root node, the program compares the target value to the node’s value. If the node and target values are the same, the program has found the target, and the search is over. If the target is less than the node’s value, the search continues down the left branch. If the target is larger than the node’s value, the search continues down the right branch. Eventually, the search either finds the target, or it tries to access a missing node. In that case, the program can conclude that the target is not present in the tree.
Figure 7 shows the code that program SortTree uses to locate nodes in its tree. This kind of search is quite fast because a tree can hold a lot of nodes while remaining relatively short. If a binary tree is evenly balanced and contains N nodes, it has a depth of around log2(N). That means the program will need to examine, at most, log2(N) nodes before it finds the target, or concludes the target is missing.
// Find a value in the node's subtree and return
// the node that contains it.
public SortedNode FindValue(int target_value)
{
if (target_value == NodeValue)
{
// We found the target.
return this;
}
else if (target_value < NodeValue)
{
// Look in the left subtree.
if (LeftChild == null)
{
// The value is not here.
return null;
}
else
{
// Make the left child search its subtree.
return LeftChild.FindValue(target_value);
}
}
else
{
// Look in the right subtree.
if (RightChild == null)
{
// The value is not here.
return null;
}
else
{
// Make the right child search its subtree.
return RightChild.FindValue(target_value);
}
}
} // End FindValue method.
Figure 7: Finding an item in a sorted binary tree.
For instance, if N = 1 million, log2(N) is roughly 20. The program would only need to examine about 20 nodes to find an item in a database containing one million records. Examining every node in order would take much longer.
Positioning NodesA program can use a similar technique to position and draw the nodes in a tree. The PositionSubtree routine, shown in Figure 8, positions the nodes within a subtree. The Point object ul gives the smallest X and Y coordinates the subtree can occupy.
// Position this subtree using the space with upper-left
// corner ul. Leave ul.x pointing to the largest X value
// used by this subtree.
public void PositionSubtree(Point ul)
{
int xmin;
Point new_point;
// Start with the leftmost position.
xmin = ul.x;
// Position the left child.
if (LeftChild != null)
{
new_point = new Point(ul.x, ul.y + BOX_HGT + V_GAP);
LeftChild.PositionSubtree(new_point);
ul.x = new_point.x;
}
else
{
ul.x += BOX_WID / 2;
}
// Position the right child.
if (RightChild != null)
{
new_point = new Point(ul.x, ul.y + BOX_HGT + V_GAP);
RightChild.PositionSubtree(new_point);
ul.x = new_point.x;
}
else
{
ul.x += BOX_WID / 2;
}
// If there no children, position this node.
if ((LeftChild == null) && (RightChild == null))
ul.x += BOX_WID;
// Position this node.
xpos = (xmin + ul.x - BOX_WID) / 2;
ypos = ul.y;
} // End PositionSubtree.
Figure 8: Positioning nodes in a subtree.
If the node has a left child, the routine invokes the left child’s PositionSubtree method to position the nodes in that subtree. If the node has a right child, the routine uses the right child’s PositionSubtree method to position the nodes in the right child’s subtree. The routine then sets the parent node’s xpos and ypos variables so it’s centered over the area occupied by its children.
The main program invokes the root node’s PositionSubtree method. When the calls to this routine finish, every node in the tree will have positioned itself correctly.
Drawing NodesThe DrawNode method, shown in Figure 9, takes as a parameter a Graphics object on which to draw. The routine draws its node in its previously assigned position. If the node’s Highlighted value is true, the routine draws it in red.
The DrawSubtree method, also shown in Figure 9, displays the nodes in a subtree. First, this routine uses DrawNode to draw its node. Then, it invokes the DrawSubtree methods for the node’s children if they exist. DrawSubtree then draws lines connecting the node to its children to make the tree structure obvious.
// Draw this node.
public void DrawNode(Graphics g)
{
String txt;
int x, y;
Pen old_pen;
Point text_size;
// If the node is highlighted, draw in red.
if (Highlighted)
{
// Save the original pen.
old_pen = g.getPen();
// Make a red pen.
Pen red_pen = new Pen(Color.RED);
g.setPen(red_pen);
}
else
old_pen = null;
// Draw a box for the node.
g.drawLine(xpos, ypos, xpos + BOX_WID, ypos);
g.drawLineTo(xpos + BOX_WID, ypos + BOX_HGT);
g.drawLineTo(xpos, ypos + BOX_HGT);
g.drawLineTo(xpos, ypos);
// Draw the node's text.
txt = String.valueOf(NodeValue);
text_size = g.getTextSize(txt);
x = xpos + (BOX_WID - text_size.x) / 2;
y = ypos + (BOX_HGT - text_size.y) / 2;
g.drawString(txt, x, y);
// Restore the original pen if necessary.
if (Highlighted)
g.setPen(old_pen);
}
// Draw the positioned subtree.
public void DrawSubtree(Graphics g)
{
// Draw this node.
DrawNode(g);
// Draw the children that exist.
if (LeftChild != null)
{
// Draw the node's subtree.
LeftChild.DrawSubtree(g);
// Draw a line connecting this node to the child.
g.drawLine(
xpos + BOX_WID / 2,
ypos + BOX_HGT,
LeftChild.xpos + BOX_WID / 2,
LeftChild.ypos);
}
if (RightChild != null)
{
// Draw the node's subtree.
RightChild.DrawSubtree(g);
// Draw a line connecting this node to the child.
g.drawLine(
xpos + BOX_WID / 2,
ypos + BOX_HGT,
RightChild.xpos + BOX_WID / 2,
RightChild.ypos);
}
} // End DrawSubtree.
Figure 9: Drawing a subtree.
Displaying TraversalsOne of the more important operations a program can perform with a tree is listing the nodes in different orders. This is called a traversal. Usually, four traversals are defined for trees: preorder, inorder, postorder, and breadth-first.
In a preorder traversal, a node lists itself before listing its child subtrees. In an inorder traversal, a node lists its left subtree, then itself, then its right subtree. A postorder traversal lists a node’s subtrees before listing the node itself. Finally, a breadth-first traversal lists all nodes at a given depth in the tree before it lists those at the next level. For example, the preorder, inorder, postorder, and breadth-first traversals of the tree shown in Figure 5 are:
preorder:56, 13, 45, 37, 48, 58, 80, 63, 95
inorder:13, 37, 45, 48, 56, 58, 63, 80, 95
postorder:37, 48, 45, 13, 63, 95, 80, 58, 56
breadth-first:56, 13, 58, 45, 80, 37, 48, 63, 95
Note that the inorder traversal of a sorted binary tree lists the items in sorted order. This gives a simple method for sorting a list of items: add them one at a time to a sorted binary tree, then produce the tree’s inorder traversal.
Figure 10 shows the preorder, inorder, and postorder traversal code used by program SortTree’s SortedNode class. These routines are quite similar in structure. Each adds the node’s value to a string, together with the traversals for the node’s children. The only difference between these routines is the order in which they combine the node’s value and the child traversals.
// Return the subtree's preorder traversal.
public String PreorderText()
{
String txt = ";
// Add this node's value.
txt += NodeValue + " ";
// Add the left subtree representation.
if (LeftChild != null)
txt += LeftChild.PreorderText();
// Add the right subtree representation.
if (RightChild != null)
txt += RightChild.PreorderText();
return txt;
} // End function Preorder.
// Return the subtree's inorder traversal.
public String InorderText()
{
String txt = ";
// Add the left subtree representation.
if (LeftChild != null)
txt += LeftChild.InorderText();
// Add this node's value.
txt += NodeValue + " ";
// Add the right subtree representation.
if (RightChild != null)
txt += RightChild.InorderText();
return txt;
} // End function Inorder.
// Return the subtree's postorder traversal.
public String PostorderText()
{
String txt = ";
// Add the left subtree representation.
if (LeftChild != null)
txt += LeftChild.PostorderText();
// Add the right subtree representation.
if (RightChild != null)
txt += RightChild.PostorderText();
// Add this node's value.
txt += NodeValue + " ";
return txt;
} // End function Postorder.
Figure 10: SortedNode traversal code.
Breadth-first traversals are a little different from the others; when it visits a node, the traversal routine cannot immediately follow the child nodes down into the tree like the other traversals do. It must first visit other nodes at the current depth in the tree. These are the node’s sibling and cousin nodes, and the node does not have a direct link to them.
Figure 11 shows the SortedNode code used by program SortTree to perform a breadth-first traversal of a tree. Note that this routine doesn’t call the BreadthFirstText method of its node’s children. To visit the nodes in the correct order, it must keep track of them more explicitly.
// Return the tree's breadth-first traversal.
public String BreadthFirstText()
{
String txt = ";
int num_waiting, num_children;
SortedNode node, waiting[], new_waiting[];
// Start with the subtree's root node in the
// waiting list.
num_waiting = 1;
waiting = new SortedNode[num_waiting];
waiting[num_waiting - 1] = this;
// Process the waiting list until it is empty.
while (num_waiting > 0)
{
// Remove the first node from the waiting list.
node = waiting[0];
for (int i=1; i<num_waiting; i++)
waiting[i - 1] = waiting[i];
num_waiting--;
// Add this node to the output text.
txt += node.NodeValue + " ";
// See how many children this node has.
num_children = 0;
if (node.LeftChild != null) num_children++;
if (node.RightChild != null) num_children++;
// Add this node's children to the waiting list.
if (num_children > 0)
{
// Make room for the new list.
new_waiting =
new SortedNode[num_waiting + num_children];
for (int i=0; i<num_waiting; i++)
new_waiting[i] = waiting[i];
// Add the children to the list.
if (node.LeftChild != null)
new_waiting[num_waiting++] = node.LeftChild;
if (node.RightChild != null)
new_waiting[num_waiting++] = node.RightChild;
waiting = new_waiting;
new_waiting = null;
}
}
return txt;
} // End BreadthFirstText.
Figure 11: Code to perform a breadth-first traversal.
The routine begins by adding the tree’s root node to the waiting array. While the array is not empty, the routine removes the first node from the array and adds it to the return text. It then adds the node’s children to the array. All the nodes at the same level in the tree are added right next to each other in the collection, so they are later removed together before any of their children are removed. That is what creates the breadth-first order of the output.
ConclusionThis article hardly scratches the surface of the things you can do with trees and other dynamic data structures. You can quickly add, remove, and rearrange the items in a tree to represent new relationships. With a little extra work, you can build more exotic kinds of trees like B-trees, B+trees, and AVL trees. These trees use re-balancing techniques to ensure that they never grow too tall and thin, and that keeps them efficient. Many commercial databases use B-trees or B+trees to allow fast access to indexes.
Using tree data structures like these, you can represent and manipulate data with complex hierarchical relationships.
The example SortTree program referenced in this article is available for download from the Informant Web site at http://www.informant.com/ji/jifile.asp. File name: ji9903rs.zip.
Rod’s books Ready-to-Run Visual Basic Algorithms, Second Edition [1998] and Ready-to-Run Delphi 3.0 Algorithms [1998], from John Wiley & Sons, have a lot more to say about different kinds of trees and many other dynamic data structures. Learn more at his Web site (http://www.vb-helper.com), or e-mail him at RodStephens@vb-helper.com.