Ruediger R. Asche
Microsoft Developer Network Technology Group
Created: January 14, 1994
Click here to open or copy the files in the DLDETECT application for this technical article.
Following up on the article "Detecting Deadlocks in Multithreaded Win32 Applications," this article describes the implementation of DLDETECT.EXE, a Microsoft® Foundation Class Library (MFC) application that aids developers in analyzing the properties of their multithreaded applications. DLDETECT implements a full-fledged Petri net editor—that is, an application that lets the user load, edit, and save Petri nets, as well as determine their dynamic properties. In the article "Putting DLDETECT to Work," we will show how DLDETECT can also be employed to convert an application into a Petri net.
It is strongly recommended that you become familiar with the material covered in "Detecting Deadlocks in Multithreaded Win32 Applications" to make best use of this article.
DLDETECT started out as a byproduct of my research on Petri nets. I was tired of redrawing the same nets and calculating the same incidence matrices over and over again, so I started writing a few routines to do the matrix calculations for me and also used the Win32® Software Development Kit (SDK) to write a small application that I could use to design nets. You know the kind of thing—nothing big, just something quick and dirty so that we can really work with incidence matrices and Petri nets instead of spending hours and hours computing them manually.
Famous last words.
After having defined some C++ structures to describe places and transitions as well as a dynamic-link library (DLL) that implements matrices, I set out to implement a File Save feature to be able to save Petri nets to disk and reload them, and that did it. Tired of filling in an OPENFILE structure for the zillionth time in my career as a professional computer abuser, I decided to give the Microsoft® Foundation Class Library (MFC) a shot because, after all, MFC is supposed to do a lot of stuff for you, and I was on the C++ track anyway, right? No more checking to see whether a file is dirty and, if yes, bringing up a Save dialog box before allowing the user to open a new file, and if the user chooses a file that already exists, prompting to replace the file, and so forth; no more learning the multiple document interface (MDI) or cutting and pasting your own scroll bar logic into yet another application where you originally wanted to do something totally different from user interface stuff.
If you are tired of hearing yet another MFC conversion testimonial, you may safely skip this introduction. But if you have not yet bothered to really look into MFC, I strongly urge you to do so. As someone who is more interested in the low-level aspects of computers, I used to hate prototyping tools and every additional layer of software that would alienate me from the real guts of the operating system. But by the same argument, I used to be annoyed by having to cope with dialog boxes, the ins and outs of device contexts, and all the work you have to put into making a user interface foolproof; basically, all I wanted to do was display something interesting (such as performance figures for bimodal interrupt handlers as compared to interrupt handlers in a VxD) in a window without all of the hassle of having to set up a message loop on my own, and so on.
And so I, too, became an MFC-phile. What I love about MFC is that you can totally control the degree to which you let MFC take over functionality for you. The first MFC version of DLDETECT was basically the original Win32® Software Development Kit (SDK) version that I wrote with a little MFC in it. All I did was have MFC create a main window for me; then I cut and pasted the code from the WM_PAINT, WM_LBUTTONDOWN, and WM_COMMAND case switches of the window function into the OnPaint, OnLButtonDown, and corresponding command handler functions of the MFC application. That worked like a charm. Then I discovered that instead of OnPaint, I should probably have put my drawing code into the OnDraw member function because then I'd get the pointer to the device context (DC) for free. Otherwise, I'd have to obtain the pointer indirectly through the CWnd's this pointer. If you are using OnDraw and need to set up your DC before drawing, you can also intercept OnPrepareDC.
Then, piece by piece, I added a document, two different views, the complete file open/save/new interface, MDI, and scrolling functionality to the application. In each of these steps I discovered that you can do things "the SDK way" if you wish, but it is very likely that MFC already provides some mechanism for doing exactly what you want. For example, in order to open a file, you could intercept the OnFileNew command handler function, or hook yourself into the OnNewDocument handler. With OnNewDocument, you will not need to initialize and display the Open dialog box. And if you do not need any fancy file input/output (I/O) features (which I did, because I used memory-mapped files—not currently supported by MFC—in my File Open processing code), you can even wait to incorporate your File Save or File Open logic until MFC calls your Serialize routine, to which it conveniently passes an archive object. When that occurs, all you need to do is add the logic to load your data from file into memory or vice versa.
I am absolutely sure that there are elements somewhere in DLDETECT that do not take full advantage of the MFC framework and might work even better if I had used MFC for them. So powerful is MFC that it provides almost anything you will ever want, and you might not even be aware of it. Although the learning curve for MFC may be fairly steep, depending on how deeply you wish to dig into it, it is definitely worth the effort to learn it. As you can see, I am enthusiastic about MFC!
But enough of this talk. What I want to do in this paper is describe the implementation of DLDETECT for you; in the paper "Putting DLDETECT to Work," I will demonstrate how any multithreaded application can be rewritten to a Petri net with the help of DLDETECT, and how you can also employ DLDETECT to analyze the run-time behavior of your application, possibly locating deadlock or race conditions.
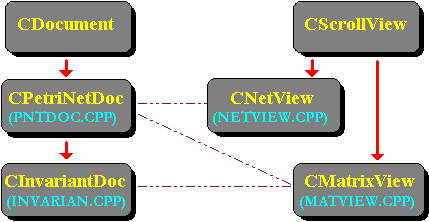
The user interface of DLDETECT is made up of four classes: CPetriNetDoc (an MFC class derived from CDocument that describes a Petri net), CInvariantDoc (a class derived from CPetriNetDoc), and CNetView and CMatrixView, two classes derived from CScrollView that allow you to view a Petri net as a net or a matrix, respectively. Figure 1 displays the class hierarchy of DLDETECT.

Figure 1. Application architecture of DLDETECT.EXE
Parts of the interface have been modeled after the most excellent explanations in the technical article "Multiple Views for a Single Document" (MSDN Library Archive, Technical Articles). Just like Tangram, DLDETECT provides a multiple document interface that lets you view a net both as a matrix and in two different windows at the same time. The section "The Application Architecture of DLDETECT.EXE" elaborates on this structure.
The logical split of the views into one matrix view and one net view nicely reflects the fact that Petri nets can be analyzed in terms of either net properties or matrix equations. Consequently, there are data structures for both Petri nets (that is, C++ classes that represent places and transitions, respectively—these are defined in CLASSES.CPP), as well as a class definition for a matrix (MATRIX.CPP). The matrix class is, in fact, fairly generic; all kinds of matrix manipulations, such as scalar multiplication or linear combination, are encapsulated in that class. I have implemented the matrix class in a DLL so that you can easily link it against an application of your own if you need to do matrix manipulation.
The next section of this paper describes the implementation of the matrix and net data structures, respectively, while the final section describes the interaction of those data structures with the application interface in terms of the view and document classes.
In this section, I discuss the non-MFC data structures that I used in DLDETECT—the matrix class and the Petri net classes, place and transition.
MATRIX.DLL, the module that deals with matrix manipulation, is pretty straightforward. It contains routines to create and delete matrix objects and to perform the most common operations on matrices: setting and retrieving matrix elements, multiplying rows and columns by integer constants, replacing rows and columns by scalars, and adding weighted scalars to rows and columns. The interesting functionality that is implemented in the DLL is the FindNullSpace member function that, when given a matrix as an argument, will determine the basis of the invariant vector space and return it as a matrix. The algorithm adopted to accomplish this was taken from Donald Knuth's invaluable collection of algorithms entitled The Art of Computer Programming, Vol. 4, Section 4.6.2, "Factorization of Polynomials," pages 425-427. Note that the general solution to the problem of finding integer solutions to the null space is NP-complete; that is, finding the null space may require an impractical amount of time and memory for large nets. For Knuth's null space algorithm, this case applies if a particular transformation of a matrix leaves any integer value other than 0, –1, or 1 in a pivot place of the matrix. If this happens, the scalar multiplier for the next iteration would have to be chosen as noninteger (namely, 1 divided by the pivot element). Ideally, the algorithm would backtrack here and try to find another, less pathological, solution.
In our case, however, there are a few characteristics that make this case unlikely to occur. First of all, we require that all nets we consider be "1-conservative"; that is, at no time will any place be marked with more than one mark, and consequently, at no point in time can a transition remove more than one mark from a place or put more than one mark into a place. (As we will see in "Putting DLDETECT to Work," this complicates rewriting your application into a Petri net a little, but makes the arithmetic a lot easier.) Thus, the incidence matrix will never have anything but 1s, –1s, or 0s in it, and all scalar manipulations on matrices that consist of 1s and 0s only will never yield a noninteger solution.
It may still happen, however, that in the course of rearranging the matrix, a value different from 1, –1, or 0 may pop up in the matrix, rendering progress in determining the null space difficult at the very least. Consider Figure 2, a screen shot from DLDETECT.EXE.
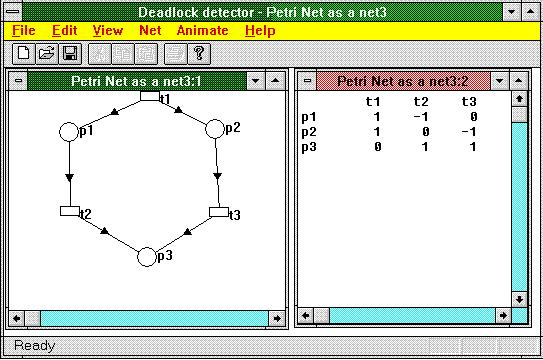
Figure 2. Pathological net
Applying Knuth's algorithm to this matrix would leave us with a 2 in the first column of the last row after the second iteration. However, the 2 would be the only element left in that column, so that by multiplying the column by 0.5 (which is a valid matrix operation), we are back to a column of only 1s and 0s. The matrix member functions AddScalarToRow and AddScalarToColumn automatically detect whether a row or column can be simplified this way after having been updated. If, after all, FindNullSpace finds a pivot element that is not 0, –1 or 1, it fails instead of backtracking. In practice, I haven't been able to construct a net in which this happens.
CLASSES.H contains declarations for all the object types that make up Petri nets, and CLASSES.CPP implements them. The class hierarchy is pretty straightforward; the base object class is a linked list object from which both the TPLIST class (the class that defines the connections between places and transitions) and the TP class (the common root class for places and transitions) derive, as shown in Figure 3.
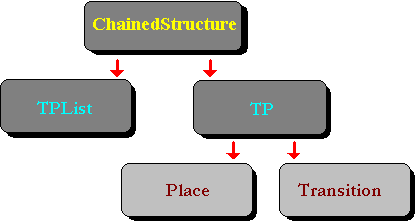
Figure 3. Non-MFC object hierarchy in DLDETECT
Initially, I merely wanted to provide a C++ framework in which places and transitions knew how to render themselves on the screen and keep track of their connections with one another. Thus, originally there was only one class, TP, which had one member variable, iType (which could take up either TYPE_TRANSITION or TYPE_PLACE as a value in a given instance), and the drawing and connecting was the same for all objects, except that one object type would display itself as a square and the other one as a circle. Each object was associated with a linked list that enumerated all other objects to which this object was connected.
However, it turns out that the differences between places and transitions are too significant to keep up this framework. When I decided to put an animation feature—specifically, having the net simulate a possible flow of execution—into the feature spec, I found that a straightforward connection scheme does not work very well. Thus, the transitions are prepared to become "live objects" in a later release. (Please refer to the article "Using Multithreading and C++ to Generate Live Objects" for details.) The thread function of those "live" transitions would need to check continually whether the transition was fireable (that is, all of its input places were marked and all of its output places were unmarked), and if so, the thread function would simulate the firing (that is, would remove all marks from the transition's input places and put marks on its output places). This functionality requires that all connections from or to any transition be visible to that transition, so I rewrote the class library in such a way that transitions are associated with two linked lists—one for a list of places leading into the transitions (the field transition::backwardlink) and one for a list of places into which the transition connects (transition::forwardlink).
Note that the only place where the Petri net data structures can be "seen" is the CNetView class. The class that is used to display a net as a matrix (CMatrixView) is not concerned with this data structure. (I'm lying! Check the architecture section for the inevitable exception. . . .)
Places and transitions are fairly self-contained; that is, all one needs to know in order to understand them can be found in their class implementation file, CLASSES.CPP. All places that belong to a particular net are collected on a linked list whose root (declared as place m_places) is a member variable in an instance of the CNetView class, and likewise, all transitions are collected on a linked list called m_transitions. When the view needs to redraw the net, it simply passes its device context to the first place that renders itself and then passes the device context on to the next place; this is repeated until all places have drawn themselves.
The view then repeats the same process for the transitions, but this time the drawing routine for a transition not only draws the transition itself but also draws all the connections between that transition and its connected places. Thus, the device context is handed down from one place to the other and then from one transition to the other, and the view itself does not become involved in drawing at all.
By drawing connections only from transitions to places, we also solve the tricky problem of knowing where to stop drawing a line. Let us look at that right after we have discussed the arrowheads.
Likewise, when the view wants to figure out whether a mouse click from the user occurred over a place or a transition, it merely calls into the Hittest member function of the first place on the list, passing only the mouse coordinates. The place checks to see whether the coordinates point to somewhere in its current image position; if yes, it returns its own this pointer to the caller, and if not, it passes the request on to the next place on the linked list. If no place responds positively to the hit-test request, the same procedure is repeated with the transitions. Once more, the view does not provide any logic to aid the hit test; it merely asks the places and transitions if anyone on those lists happens to be under the point where the cursor was when the mouse button was clicked.
Using the approach where chained objects pass DCs on to each other, it does not really matter to the view what the editable objects are; by substituting the class library for places and transitions by a library for, say, Tangram pieces, we can basically put the same application to work on Tangram pieces, as long as the Tangram objects support the DrawYourself and Hittest member functions.
Believe it or not, one of the hardest problems to solve while developing DLDETECT was to compute how to draw the arrowheads on the connecting lines. I spent a few days figuring out how to do it; had I paid attention in trigonometry classes, it would have gone a lot faster. Oh well. . . . Note that I did not attempt to find a general solution, such as any arrow of any pointiness on any point of the line; I was perfectly satisfied with an equal-sided triangular arrowhead right on the middle of the line. Here is how to do it.
Drawing arrowheads
We are interested in four points of the arrowhead: the center point (xc, yc), around which we want to draw the arrowhead, and the three points, (x1, y1), (x2, y2), and (x3, y3), where (x1, y1) describes the "target point," which is on the line along with the center point. See Figure 4 for a graphical representation of this.
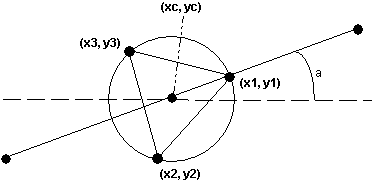
Figure 4. Drawing an arrowhead
You first compute the center point (xc, yc). This is easy because we are dealing only with straight lines: The center point is exactly halfway on the line—that is, its x coordinate is exactly in the middle, between the x coordinates of the beginning and the end of the line, respectively; and the same is true for the y coordinate.
As for the other three points, note that because we are dealing with an equilateral triangle, they all lie on the circumference of the circle surrounding (xc, yc) with a radius of DELTA, where DELTA is a constant that describes how chunky we want the arrow to be. Thus, each of the points (x1, y1), (x2, y2), and (x3, y3) can be expressed by the trigonometric equation
sin a + cos a = DELTA
if we take (xc, yc) as the center of the coordinate system and a as the angle formed with the horizontal of one of the lines ended by that point.
First, you need to find the point (x1, y1). To do this, you compute the sine and cosine of the angle that corresponds to the slope of the line so that the arrowhead point can be aligned with the line itself. Fortunately, we do not need the angle itself but can express the sine and cosine in terms of the tangent, and the tangent itself is the same as (tadaaaaa!) the slope, which we know because we know the beginning and the end of the line: The sine is the same as the tangent divided by the square root of 1 plus the tangent squared, and the cosine is the same as 1 divided by the square root of 1 plus the tangent squared.
In an equilateral triangle, all angles are 60 degrees. Thus, after obtaining (x1, y1), one can express (x2, y2) by the sine and cosine of the sum of 60 and the angle that the first point forms with the horizontal, and (x3, y3) as the sum of 120 and that same angle. Fortunately, we can rewrite the appropriate trigonometric equations as follows:
sin (a + b) = sin a * cos b + cos a * sin b
and
cos (a + b) = cos a * cos b – sin a * sin b.
The sine and cosine of a are known because we computed them beforehand for (x1, y1), and b is constant (namely, 60 for the second point and 120 for the third point), and thus, their respective sines and cosines are also constants. Thus, arrowheads can be drawn fairly efficiently using only the center point of the line and a few constants.
Just for the sake of completeness, I list here the relevant code for drawing the arrowheads; you will find the complete code in CLASSES.CPP (transition::DrawYourself).
#define DELTA 5.0
#define COS120 -.5
#define SIN120 .866025 // Determined by a calculator...
#define COS240 COS120 // See note immediately following code.
#define SIN240 SIN120*-1.0
float iSlope;
if (iX==iTargetX) iSlope=0; else iSlope=(float)(iTargetY-iY)/(float)(iTargetX-iX);
// Now compute the middle of the line, so we can draw the arrowhead around it.
iCenterX=((abs(iTargetX-iX))/2+min(iX,iTargetX));
iCenterY=((abs(iTargetY-iY))/2+min(iY,iTargetY));
iNewX=(float)(1/sqrt(1+(iSlope*iSlope)));
iNewY=(float)(iSlope/sqrt(1+(iSlope*iSlope)));
if (iCenterX==iTargetX)
{
iNewX=0;
iNewY=(iTargetY>iCenterY) ? (float)1 : (float)-1;
}
else
if (iCenterX>iTargetX) {iNewY*=(float)-1; iNewX*=(float)-1;};
// Assign the arrowhead coordinates.
ptArrow[0].x= (int)(DELTA*iNewX)+iCenterX;
ptArrow[0].y= (int)(DELTA*iNewY)+iCenterY;
ptArrow[1].x= (int)(iNewX*COS120*DELTA-iNewY*SIN120*DELTA)+iCenterX;
ptArrow[1].y= (int)(iNewX*SIN120*DELTA+iNewY*COS120*DELTA)+iCenterY;
ptArrow[2].x= (int)(iNewX*COS240*DELTA-iNewY*SIN240*DELTA)+iCenterX;
ptArrow[2].y= (int)(iNewX*SIN240*DELTA+iNewY*COS240*DELTA)+iCenterY;
// Draw the arrowhead.
hDC->Polygon(ptArrow,3);
Note The symbolic constants read 120 and 240, instead of 60 and 120 degrees as they should. This was the result of a momentary lapse on my part; however, because the sine of 240 is the same as –1 * sin 60 and cosine of 240 is the same as –1 * cos 60, the computations still yield the correct results. Isn't trig wonderful?
Knowing where to stop
Although the connection between a transition and a place is basically a straight line, we cannot draw the connection line from the center of a transition to the center of a place because the line would draw over parts of the objects. DLDETECT solves this problem this way: It first draws all the places, and then for each transition, it draws all connections to and from that transition, before drawing the transition itself. The rectangle that represents the transition will erase all the pieces of the lines that would have interfered with its body because the rectangle is painted with a white opaque brush. Using some trigonometry, the transition painting logic knows where to stop drawing the line on the other end (that is, the place's end). Because a place is represented by a circle, each point on the circumference of the circle can be described in terms of the sine and cosine of the angle of the line that intersects with it, and because we know the angle that the connecting line forms with the horizontal (as discussed before, we know the tangents because we know the slope of the line by its start and end points), we can compute the sines and cosines and, therefore, the absolute coordinates where the line hits the circle. (The reasoning here was explained before in the discussion on drawing the arrowheads.)
iNewX=((float)1.0/(float)sqrt((float)1.0+((float)iSlope*(float)iSlope)));
iNewY=((iSlope<0?iSlope*(float)-1.0:iSlope)
/(float)sqrt((float)1.0+((float)iSlope*(float)iSlope)));
if (iX==iTargetX) {iNewX=0; iNewY=1;}
if (iX<iTargetX) iNewX*=(float)-1.;
if (iY<iTargetY) iNewY*=(float)-1.;
iTargetX+=(int)(iNewX*((float)PLACEXEXTENSION/2));
iTargetY+=(int)(iNewY*((float)PLACEYEXTENSION/2));
hDC->MoveTo(iX,iY);
hDC->LineTo(iTargetX,iTargetY);
In this section, I will describe the application architecture of DLDETECT a little bit more in detail. The major user interface challenge I faced when writing the application was to sort out the subtle differences between Petri net matrices and net invariant matrices. A Petri net is internally implemented as a document object (CPetriNetDoc) that has two possible views—a view as an editable net (CNetView) and a view as a matrix (CMatrixView), with the net view being the "primary" view (that is, the view that is generated by default when a new document is created). As mentioned before, the net view and the matrix view were designed to be as independent as possible; that is, they do not share any data explicitly. When the matrix view displays itself, however, it must be able to access data from the net view: In this case, the matrix view must have access to the names of the transitions and places to label the matrix. In order to make the interactions between the views as clean as possible, each request from one view to the other must go through the document, as illustrated in Figure 5.
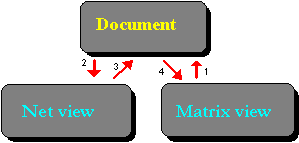
Figure 5. The matrix view calls into the document to obtain data from the net view.
Thus, the matrix view, when asking for the name of an object, calls into the document, which in turn dispatches the call to the net view. This way, by overriding the dispatcher function in the document class, the behavior can be updated as desired without hard-coding the relationship between the views. We'll look at how DLDETECT does this later on.
The net invariants are computed in the context of a document type that behaves differently from the Petri net. The trick here is that I derive a class from CPetriNetDoc, called CInvariantDoc, that behaves pretty much like the Petri net document in that it has both an associated net view and a matrix view, but this document type never displays its net view. Upon creation of the application, three new CMultiDocTemplate objects are created.
m_pNetTemplate= new CMultiDocTemplate(IDR_NETMENU,
RUNTIME_CLASS(CPetriNetDoc),
RUNTIME_CLASS(CMDIChildWnd), // Standard MDI child frame
RUNTIME_CLASS(CNetView));
AddDocTemplate(m_pNetTemplate);
m_pMatrixTemplate= new CMultiDocTemplate(IDR_MATRIXMENU,
RUNTIME_CLASS(CPetriNetDoc),
RUNTIME_CLASS(CMDIChildWnd), // Standard MDI child frame
RUNTIME_CLASS(CMatrixView));
AddDocTemplate(m_pMatrixTemplate);
m_pInvTemplate= new CMultiDocTemplate(IDR_MATRIXMENU,
RUNTIME_CLASS(CInvariantDoc),
RUNTIME_CLASS(CMDIChildWnd), // Standard MDI child frame
RUNTIME_CLASS(CMatrixView));
AddDocTemplate(m_pInvTemplate);
Two of these templates, m_pNetTemplate and m_pMatrixTemplate, are associated with the CPetriNetDoc document class, and the third one, m_pInvTemplate, with the CInvariantDoc document class. In order to create an invariant view, the logic that responds to the user clicking "Find Net Invariants" from the matrix view calls the following sequence in MATVIEW.CPP:
void CMatrixView::OnNetFindnetinvariants()
{ CInvariantDoc *cpnNewDoc;
matrix *mtTemp=GetDocument()->m_mCurrentMatrix->Copy();
if (mtTemp == (matrix *)0)
{AfxMessageBox("Problem copying the matrix...");
return;
};
matrix *mtTemp1=mtTemp->FindNullSpace();
delete (mtTemp);
if (mtTemp1 == (matrix *)0)
{AfxMessageBox("Could not determine null space of matrix...");
return;
};
cpnNewDoc = (CInvariantDoc *)theApp.m_pInvTemplate->OpenDocumentFile(NULL);
cpnNewDoc->SetTitle("Net invariants for "+GetDocument()->GetTitle());
cpnNewDoc->m_mCurrentMatrix=mtTemp1;
cpnNewDoc->cnvAttachedView=GetDocument()->cnvAttachedView;
cpnNewDoc->cmvAttachedView->OnUpdate(NULL,0,NULL);
}
Note that if we opened a document file from the CPetriNetDoc class, we would end up with a net view of the document; we force a matrix view to be displayed by calling this instead:
theApp.m_pInvTemplate->OpenDocumentFile(NULL),
The CInvariantDoc class automatically disables the View/As a net menu item such that the net view will never be displayed. However, we set the attached net view of the new invariant document to the current net view so that the invariant document can query the current net for information. This is where the "indirect" communication between the views (as described earlier) comes into play: When the matrix view queries the document for the name of a place or transition object, it calls into the document's GrabNameFromNet member function. For the CPetriNetDoc base class, this function routes the call on to CNetView::GrabNameFromNet for both places and transitions, but for invariant matrices, we want the rows to be labeled with the places' names but the columns with the invariant name. Thus, for the CInvariantDoc class, we override the GrabNameFromNet function to do the same thing the base class CPetriNetDoc did before for the rows, but to generate unique names for the columns:
CString CPetriNetDoc::GrabNameFromNet(BOOL bType, int iIndex)
{
CString csResult= cnvAttachedView->GrabNameFromNet(bType, iIndex);
if (csResult.GetLength() <5)
csResult+=" ";
return csResult;
}
CString CInvariantDoc::GrabNameFromNet(BOOL bType, int iIndex)
{
if (bType)
{CString csResult= cnvAttachedView->GrabNameFromNet(bType, iIndex);
if (csResult.GetLength() <5)
csResult+=" ";
return csResult;
}
else
{char szBuf[5];
sprintf(szBuf,"I%d",iIndex);
CString csResult = (CString)szBuf;
BOOL bToggle=FALSE;
while (csResult.GetLength() < 5)
{if (bToggle)
csResult=" "+csResult;
else
csResult+=" ";
bToggle=!bToggle;
};
return csResult;
};
}
Using the application design framework provided by the Microsoft Foundation classes, in particular the document/view structure, I found that implementing DLDETECT.EXE was a fairly straightforward task that left most of the design work focused on the application's functionality (that is, Petri net properties) instead of on the user interface. As mentioned before, through the "chained draw and hit-test functionality," the application can be modified fairly easily to work on any objects that can be kept in a linked list and support self-drawing and hit testing.
Even though the application currently lacks some important features, such as simulating control flow and keeping track of resource allocation graphs, I found it to be very useful for getting a better understanding of the properties of multithreaded applications. The article "Putting DLDETECT to Work" elaborates on some of those results.
DLDETECT.EXE can be enhanced in a number of ways. If you find the application to be useful and would like to see features added, please contact me via one of the contact points listed in the Microsoft Developer News and wait for the next edition of the Development Library to be released; alternatively, you might want to rewrite DLDETECT.EXE yourself. If you add anything really cool, I'd love to see it!
If I were to keep working on DLDETECT, here is the list of features that I would add:
Asche, Ruediger. "Detecting Deadlocks In Multithreaded Win32 Applications." Microsoft Development Library, 1994.
Asche, Ruediger. "Putting DLDETECT to Work." MSDN Library, 1994.
Asche, Ruediger. "Using Multithreading and C++ to Generate Live Objects." MSDN Library, 1993.
Crain, Dennis. "Win32: Hit Testing Lines and Curves." MSDN Library, 1994.
Rogerson, Dale. "Multiple Views for a Single Document." MSDN Library Archive, 1993.
Knuth, Donald E. The Art of Computer Programming. Reading, MA: Addison-Wesley, 1973.